BP 神经网络在汇率预测中的应用

徐缘圆

（中南财经政法大学，湖北 武汉 430079）

一、研究背景与研究方法

所谓汇率（又称外汇利率，外汇汇率或外汇行市），是指两种货币之间的对换的比率，同时也可视为一个国家的货币对另一种货币的价值。汇率与一国进出口、物价、资本流出入都有着密不可分的关系，会因为利率、通货膨胀、国家的政治和每个国家的经济等原因而变动。根据国际货币制度的演变，汇率可以划分为固定利率和浮动利率。在Bretton Woods system 崩溃后，世界上汇率制度渐渐变成以浮动汇率制度为主，汇率变动更是显现出动态化和复杂化的特征。特别是在全球经济一体化的背景下，各国之间的联系日益密切，相互之间的依赖性也越来越强，汇率，自然地成为各国之间经济往来的桥梁。然而，各国的外汇管理和货币政策的实施效果受到了汇率的变化的严重干扰。在此背景下，探寻人民币兑美元汇率的变化特征以及其内在的运行规律，对汇率进行准确的预测就有了诸多现实意义。

对汇率预测方法的研究主要有技术分析和基本分析。以基本分析方法为基础的汇率预测应用非常之广，其中包括很多很经典的方法理论，比如，以购买力平价理论、利率平价理论、资产市场组合模型为代表的传统的汇率理论及模型，以基于新开放宏观经济学的汇率理论、混沌分析理论、基于检验外汇市场有效性的汇率理论等为代表的新近发展起来的汇率理论。技术分析经历了参数到非参数，线性到非线性的发展过程，其中，参数方法主要包括随机游走模型、自回归移动平均模型、自回归条件异方差模型、自我激励阀值自回归模型、指数平滑过渡自回归模型等。非参数方法主要包括小波分析、遗传算法、人工神经网络等。

近年来，非参数方法中的神经网络技术的出现，极大地提高了汇率预测中的样本拟合度。其中，按误差逆传播算法训练的多层前馈网络——BP 神经网络，更加能够直接生动地反映系统的动态特性，因此它更适合对具有非线性的、动态的特征的汇率系统进行预测。

二、实证研究

理论上，一个三层的神经网络就能够以任意的精度逼近连续函数，也就能满足实证建模的需要。尽管欧元等其他主要货币的比重也在逐渐上升，但是中国的储备货币目前仍然是以美元为主，因此，若是能够对人民币兑美元汇率进行准确地预测，货币当局就能更好的把握人民币和主要储备货币之间复杂的变动关系，进而灵活地、有针对性地对储备货币的结构进行调整，从而做好外汇风险的防范工作。在本文中，将采用单步预测法对人民币兑美元中间价进行预测，这不仅有助于我国汇率政策、利率政策等的制定和调整，也有助于企业进行科学的国际贸易决策。

（一）数据选择

本文实证研究将选择2010 年01 月04 日起至2012 年10 月25 日为止央行公布的每日人民币兑美元汇率中间价，一共680 个数据为样本，进行实证研究 (所有数据均来源于中国人民银行网站：http://www.pbc.gov.cn/)。 之所以取2010 年至2012 年近700 个数据，原因如下：

一方面，人民币兑美元汇率是一组时间序列数据，对于它的预测工作，当然是时间上越近的数据越有代表性，预测结果更有说服力；

另一方面，Kang 在利用神经网络对时间序列进行预测的研究中就指出了，要想模型有较好的预测能力并不一定必须要具备很大的数据样本。再后来，Walczak 以不同规模的数据样本，利用神经网络模型对汇率序列进行预测后，通过比较结果，得出在多数情况下两年的数据样本就足以使神经网络模型产生合适的预测精度这一结论。

（二）构造训练样本

把前679 天的数据按顺序输入，作为网络的一个输入数据（即把样本数据从第1 个取到第679 个，作为p），然后将后面的679个数据输入，作为网络输出即目标数据（即从第2 个取到第680 个，作为t），按这个方式进行滚动式的排列，就形成了神经网络的训练样本。

（三）选用三层结构的BP 神经网络建立预测模型

理论上，一个三层的神经网络就能够以任意的精度逼近连续函数。由于其具有操作性强、计算量小等优点，目前仍是多层式网络训练的首选网络结构之一，并且已经被人们推广应用于各种各样实际问题的解决中。因此，我将在本论文中采用三层网络建立模型进行汇率预测。

输入层和输出层的节点数主要由输入变量决定，这些将直接影响网络的学习效果和泛化能力。对时间序列预测问题，输入层节点数等于所开窗口大小，在本例中输入层节点数即为679，加之本文只限于一维时间序列，所以预测值只需要用一个输出层节点来表示，本例中输出层节点数为1。隐藏神经元主要应用于学习数据的内部规律，试凑法是确定最佳隐藏层节点数的一个常用方法，即先用较少的隐层节点数进行训练，然后逐渐增加隐藏层节点数，用同一样本集进行训练，从上述训练结果中选出网络误差最小的一组确定为隐藏层节点数。在用试凑法的时候，也可以用一些经验公式来确定隐藏层节点数。用这些公式计算出来的隐层节点数的粗略估计值，可以作为确定隐层神经元数目初始值的大致参考。

即隐藏层节点数为28—37 中的一个整数。

在MATLAB 中进行训练，得到训练结果如下，见表1：

表1 训练结果

网络误差最小所对应的隐层神经元个数为28，因此，本例中b即为28。

（四）预测过程的具体实现

建立一个新的前向神经网络，%设置网络隐单元的神经元数、输出层节点数及训练函数net=newff(minmax(p)，[28，1]，{‘tansig’，’purelin’}，’traingdm’)；% 当 前 输 入层 权 值 和 阈 值inputWeights=net.IW{1，1}，inputbias=net.b{1}；%当前网络层权值和阈值layerWeights=net.LW{2，1}，layerbias=net.b{2}；%设置训练参数net.trainParam.show=50，%每50 步显示一次误差，net.trainParam.lr=0.05，%训练步长，net.trainParam.mc=0.9，%Sigmoid 参 数0.9，net.trainParam.epochs=10000，% 最大训练次数，net.trainParam.goal=1e-3，%设定的期望误差，一般为0.001；%调用TRAINSCG 算法训练BP 网络[net，tr]=train(net，p，t); % 对BP 网络 进行仿真p_TEST=6.3047，A=sim(net，p_TEST)；% 计算 仿 真 误 差E=t -A，MSE=mse(E)。

按上述过程在MATLAB 中进行操作后，得到误差趋势图如图1 所示：

图1 BP 神经网络训练误差趋势图

当前输入层权值和阈值、当前网络层权值和阈值部分结果（因版面问题未能全部列示）如表2 所示：

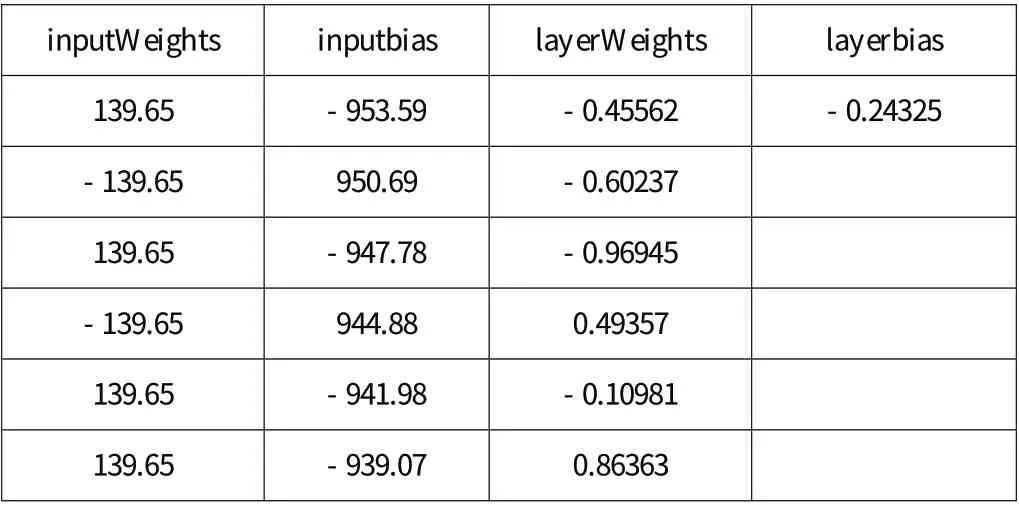
表2 输入层权值和阈值、当前网络层权值和阈值部分结果

预测值A 为6.3251，MSE=0.00099823.

2012 年10 月26 日人民币兑美元汇率中间价为6.3010，与预测值相差0.0241，误差率为0.38%，明显地，预测值与实际值相差并不是很大，说明用MATLAB 进行BP 神经网络预测模型进行汇率预测效果不错，具有可行性。

经过上述的探索操作，我们根据2010 年01 月04 日起至2012 年10 月25 日为止中国人民银行公布的每日人民币兑美元汇率中间价，共680 个数据样本预测出了下一日的汇率中间价，预测过程合理规范，并最终达到了实证目的。进一步地，还可以通过滚动预测法预测以后更多的汇率，操作思想同上，不再赘述。

尽管BP 神经网络对汇率预测效果不错，但还是存在一些不足之处。神经网络模型只利用了汇率的历史数据来进行预测，并没有考虑影响汇率变动的经济、政治等因素，也没有将其量化入模型中，故只能在外部环境较为稳定的前提下进行短期预测。此外，BP 神经网络本身也在算法上存在一些缺陷，比如它的收敛速度较慢慢、容易导致局部最小、训练结果不稳定等。

[1]丁辉，基于神经网络模型的人民币汇率预测研究，2008.

[2]王莎.BP 神经网络在股票预测中的应用研究，2008.4.

[3]赵振勇.基于遗传BP 神经网络的股市预测，2007.5.

[4]孟生旺.神经网络模型与车险索赔频率预测.统计研究，2012(03):22-26.

[5] http://www.pbc.gov.cn/中国人民银行