三体相互作用下三势阱中玻色-爱因斯坦凝聚体的稳定性研究

穆爱霞

(平凉医学高等专科学校 甘肃 平凉 744000)

1 引言

自从玻色-爱因斯坦凝聚体在实验上被观测，许多研究是关于两组分或双耦合BEC(玻色-爱因斯坦凝聚体)的隧穿现象及宏观量子自俘获，但很少研究三组分[1～5].在目前的研究中，三囚禁势阱中的隧穿特性已从理论上得到，多阱中的BEC自俘获现象也已经从实验上证明，但是其背后的相关物理实质还未曾知道.因此，要了解多阱中的非线性约瑟夫森振荡和自俘获现象是很重要的，最简单的三囚禁势阱中的BEC能更多地展示一些有趣的行为且为研究光晶格BEC提供便利[6，7].

对于相互吸引的BEC，凝聚体基态原子数会在塌缩和增长间交替变化，在这个过程中，三体复合起主要作用，塌缩和增长已通过分析GP方程而证明，通过突然改变原子之间相互作用或势阱，凝聚体易进入长期的混沌振荡.在本文中，我们讨论有三体复合耗散效应时，玻色-爱因斯坦凝聚体在三势阱中的动力学特性.在三体问题中增加任何量都会增加难度，其结果是有更复杂的非线性，且基本方程中更多参数将会在模型中引入更为丰富的动力学特性和更复杂的结构.我们将结合数值分析的方法，研究三阱中有原子填充项和三体复合耗散时BEC特性，相对粒子数的数值结果展示了自俘获现象和定态解的稳定性.

2 含三体项的三模近似

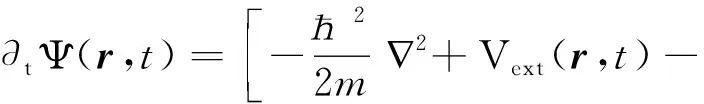
(1)

(2)

为了研究玻色-爱因斯坦凝聚体在三势阱中的动力学特性，我们采用三模近似的方法来寻找方程(2)的解

(3)

假定势垒足够高，在隧穿区域，波函数的重叠非常少，即三体玻色-爱因斯坦凝聚体之间为弱耦合时，三模近似得到了很好的应用，弱耦合时空间分布函数Φ1,Φ2,Φ3在各阱中的分布满足正交关系

(4)

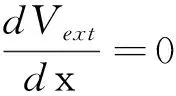
i∂τΨ1=(E1-U1|Ψ1|2)Ψ1-

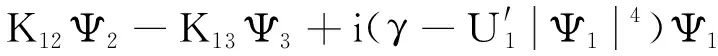
(5)

i∂τΨ2=(E2-U2|Ψ2|2)Ψ1-

(6)

i∂τΨ3=(E3-U3|Ψ3|2)Ψ3-K13Ψ1-

(7)

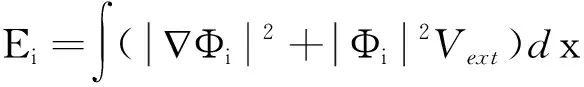
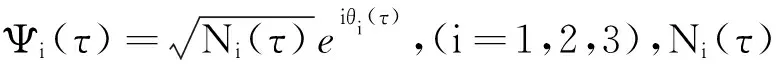
(9)

(10)

(11)

(12)

(13)

(14)

其中Φ1=θ2-θ1,Φ2=θ3-θ1,为了了解三势阱中玻色-爱因斯坦凝聚体相互作用的新现象，我们考虑理想情况，即完全对称的情况.所以，令

U1=U2=U3=U

E1=E2=E3

阱1,2之间的粒子数差和阱2,3之间的粒子数差相同，即N1-N2=N3-N2,且忽略1,3阱之间的作用，考虑1,2阱之间的隧穿率等于第2,3阱之间的隧穿率，Φ1=Φ2=Φ，K12=K23=K,则上面的方程变为

(15)

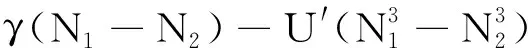
(16)

(17)

作如下变换N1-N2=Z，则式(15)～(17)变为

(18)

(19)

(20)

可以发现方程(18)～(20)不同于两阱时的情形，在方程中出现了一些耦合项不同于文献[7]中的方程(16)～(18).因此，三势阱中中间一个阱对系统的隧穿特性有重要影响，我们期望三势阱中的隧穿特性能展示与两势阱的区别.相应的数值结果将在下部分仔细讨论.原子的填充效应γ可被看做是一个线性放大，三体复合ξ同样很重要，γ,U′等于零，则N是恒定不变的.当考虑三体复合耗散时，N是随时间变化的，此时,由于γ,ξ两项的出现，凝聚体会出现新的特性.这组方程是不可积分的，且数值解仅可以通过变分等近似方法得到.下面讨论该非线性方程组解的稳定性问题，我们通过改变散射长度来改变γ，从而,由调节γ得到新的特性.

3 系统定态解的稳定性分析

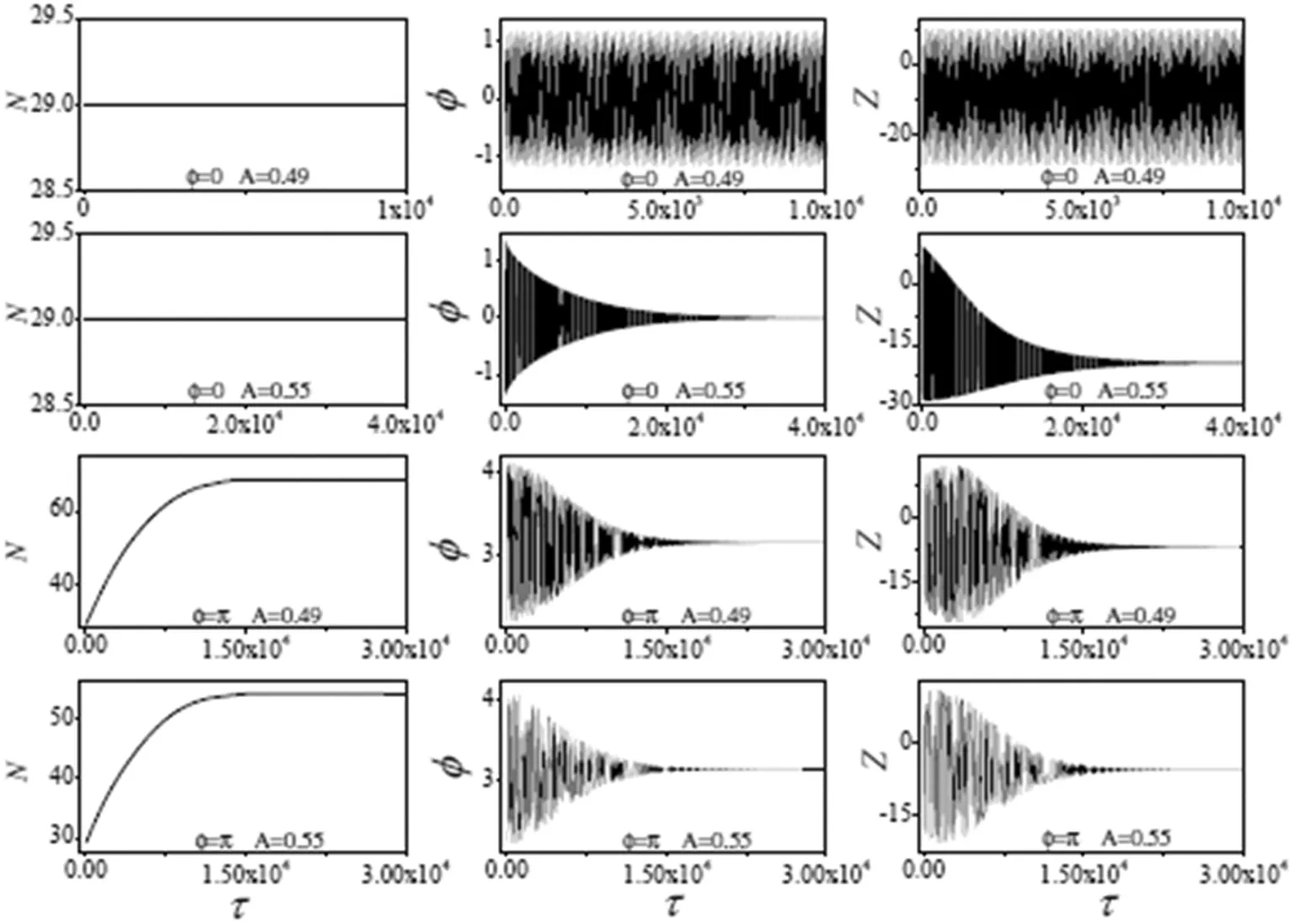
图1 初始条件为N(0)=29,Z(0)=10,Φ(0)=0,Φ(0)=π时，N,Φ,Z对应的数值解

通过图1发现，对于A=0.49,Φ(0)=0时，Φ和Z都在很大区域振荡且最终没有趋于一个定态解，但是对于A=0.55,Φ(0)=0时，Φ和Z最终都趋于一组定态解(N0=29,Φ0=0,Z0=-19.58),这些数值结果都很好地和表1对应结果一致.因此，表1中对应的A=0.49,Φ(0)=0一组定态解即为不稳定的，而表1中A=0.55,Φ(0)=0对应一组解是稳定的.图1中当Φ(0)=π时，对于A=0.49,A=0.55，N,Φ,Z最终都趋于定态解,分别为

N0=68.48,Φ0=3.14,Z0=-6.69

和

N0=54.27,Φ0=3.14,Z0=-5.67

这些解同样与表1给出的解很好地吻合.因此，表1中对应的这些解同样是稳定的.所以，我们发现初始相位对定态解的稳定性有重要影响.而且经分析发现，在图1中，当A=0.49,Φ(0)=0时原子布居数Z在Z=-10之间振荡，从数值上展示了三势阱间原子的非定态量子隧穿.而当A=0.49,Φ(0)=π时原子布居数Z在最终趋于一定值(Z=-6.69)，数值上展示了在三势阱中原子布居数Z，可以呈现高度的不对称分布，好像绝大多数原子被其中的一个阱俘获，即系统进入了自俘获态.另外，定态解的稳定性还与参数K,γ,U′,U的改变有关，我们将在以后的研究中，展示更多参数对定态解的稳定性的影响结果.

参考文献

1 Fritz London. On the Bose-Einstein condensation.Phys.Rev,1938, 54: 947

2 汪志诚. 热力学统计物理学. 北京：高等教育出版社，1993

3 Wang G F,Fu L B,Zhao H and Liu J. Self-trapping and its periodic modulation of Bose-Einstein condensates in double-well trap. Acta Phys,Sin, 2005, 54: 5003(in Chinese)

4 E.A.Donley etal.Dynamics of collapsing and exploding Bose-Einstein condensate. Nature, 2001, 412(6844): 295～299

5 Y.Kagan,E.L.Surkov,and G.V.Shlyapnikov. Evolution and Gl obal Collapse of trapped Bose-Einstein condensates under Variations of the Scattering Length. Phys.Rev.Lett., 1997,79(14) : 2 604～2 607

6 Tristram J. Alexander,Elena A.Ostrovskaya,and Yuri S.Kiv shar. Phys.Rev.Lett., Self-trapped Nonlinear Matter Waves in Periodic Potentials,2006,96:040401

7 Li Y and Hai WH. J.Phys.A:Math.gen., 2005, 38:

4 150～4 114