排水沟渠在道路排水系统中的计算分析与应用

石 鑫 ,李志勇 ，李彦伟

（1.长安大学公路学院，陕西西安 710064；2.重庆交通大学土木建筑学院，重庆 400074；3.石家庄市交通运输局，河北石家庄 050051）

0 引言

排水沟渠是道路排水系统的重要组成部分，应用于路表集中式排水（边沟及排水沟）及坡面排水（截水沟），主要起汇聚、收集、输送水流的作用。如排水沟渠应用不合理，会造成水流蔓延至路面，导致路面结构的损坏，且会影响行车安全[3]，因此排水沟渠的设计正确与否至关重要。

1 排水沟渠的形式

排水沟渠的形式可分为传统型及浅薄型。传统型包括矩形、梯形、三角形等；浅薄型有V字型、皿型及半圆形等（见图1）。

三角形边沟及抛物线型边沟是由拦水带及道路铺面构成的，两者在形式上非常类似，此类沟渠应注意控制道路的过水断面宽度，这主要取决于水流量及道路横坡大小；三角形边沟还有一种是带有低洼区的，但在公路排水中应用较少；矩形和梯形也是常用的边沟形式，对此两类，主要控制参数为沟底尺寸及沟内水流深度。

图1中，图a)的V字型常应用于道路边缘排水的边沟；图c)V字型常用于中间分隔带排水。图b)皿型和图d)半圆形因水深较小，因此同样的排水量条件下，其过水断面宽度较矩形及梯形要大，因此不太适合应用于道路硬路肩处的边沟。

2 边沟的布置形式

（1）边沟布置总体原则应根据不同路段分别设计，避免整齐划一，一刀切。

（2）边沟的布置形式分为有拦水带和无拦水带两种情况。有拦水带，道路铺面和拦水带构成浅三角形边沟，为减小过水断面宽度，可在拦水带附近采用连续或局部低洼区。由于施工的原因，前者常用于公路排水，后者则用于城市道路排水。公路常采用图2所示的带浅槽的三角形边沟以减少过水断面的宽度。

（3）对于路堤路段，本文推荐设置两种边沟形式：一是设置拦水带，由此形成浅三角形边沟；二是采用梯形或炬形边沟。由于车辆一旦向道路边缘偏离，冲入边沟，会形成较大的交通事故。因此，本文建议矩形或梯形边沟使用时要加装盖板，在盖板上开孔或留缝隙。对图1所示的皿型或半圆形边沟，不推荐在道路边缘使用，因水流量较大或流速较快时，水流会越出边沟，直接冲刷土路肩或边坡。

（4）挖方路段既有路表水，又有坡面水，如采用加装盖板的矩形或梯形边沟，坡面水流速较快时会直接流至路面，因此本文推荐在路堑路段使用如图3所示的边沟形式。

（5）如图3所示排水沟，当半径R过大，即边沟较浅时，可在边沟内设置如图4的排水口，将水流引入排水口，以避免水流宽度过宽时漫流至路面。采用此类排水口的最大问题是排水管的堵塞问题，究其原因有三个：a.运土方、煤、砂石料卡车超载严重，沿路撒落现象普遍，随雨水进入边沟而造成淤积；b.纵坡偏小而造成流速不足(10 cm内径管，要满足0.75 m/s的防淤要求，沟底纵坡至少要达到1.3%)；c.清淤困难。本文建议采用此类排水口时，可采用高压水流解决沟底的冲淤问题。

（6）如图5所采用的皿型边沟，属道路两侧的用地高于路表的路段，且距离较长，因此需要在边沟内设置排水口，以便将水引入，降低边沟内的水流宽度，防止其漫流至路表。

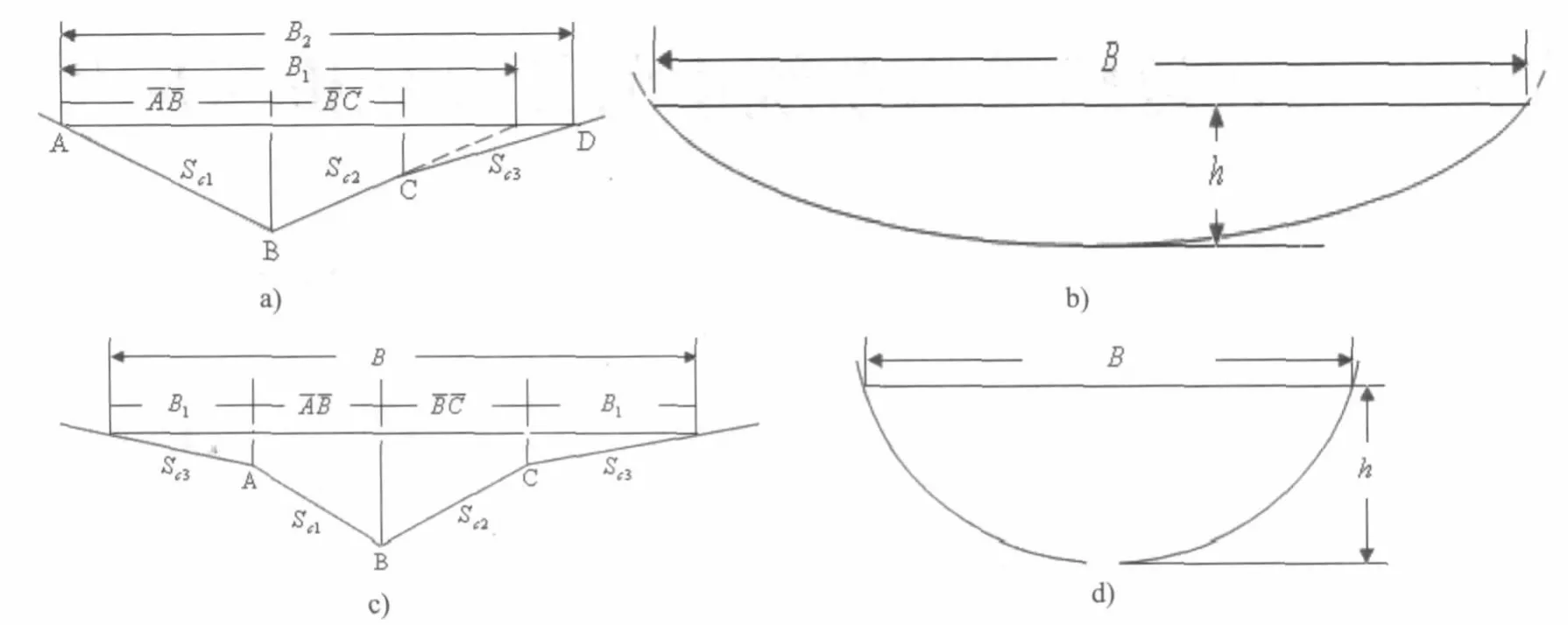
图1 浅薄型边沟示意图

图2 带浅槽的三角形边沟示意图

图3 路表路堑排水示意图

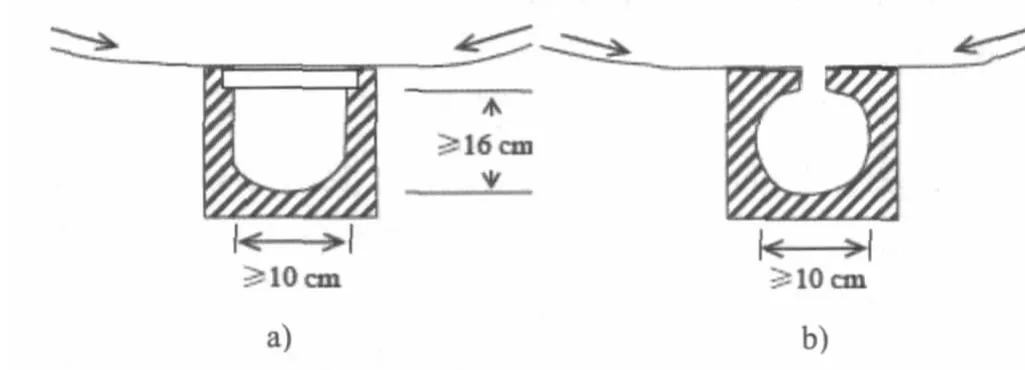
图4 边沟内设置排水口示意图

图5 皿型边沟内设置排水口实景

（7）设置边沟时，除了考虑其适用性以外，还需考虑施工难度、经济性等因素，选择合理的边沟布置形式。

3 沟渠流量计算

沟渠流量均可以通过曼宁公式进行计算，其表达式如下[1],[2]：

式中：A——过水断面面积，m2；

v——边沟内的平均流速，m/s。

边沟内平均流速按谢才公式计算：

式中：R——水力半径，m，R=A/ρ；

ρ——过水断面湿周，m；

i——水力坡度，m/m，对于沟渠，可按和沟

渠底部纵坡Sl相等进行计算；

C——流速系数，m0.5/s。可按曼宁公式计算确定：

由公式(2)可知，只要已知沟渠的过水断面面积、湿周、沟渠材料、沟渠纵坡所对应的曼宁系数，则其流量可求。

3.1 三角形边沟流量计算

对于单一横坡的浅三角形边沟，在已知水深h、铺面横坡SC的情况下，水面宽度B、面积A和湿周ρ的计算公式如下：

由于 SC很小，S2C＜＜1，h＜＜B，因此式（6）可以简化为：由此可以得出水力半径R的计算结果为：

根据上述水力参数，取道路纵坡为水力坡度，则浅三角形边沟的流量计算公式为：

对于浅三角形边沟，公路表面水的宽度有可能会超过水面深度的40倍以上，上述曼宁公式的水力半径不能准确地描述边沟的形式。因此采用修正过的曼宁公式进行流量计算，即在曼宁流速系数上乘以1.2的系数。则可以得到规范中推荐的浅三角形边沟流量计算公式[1]：

由公式（4），式（10）可改为：

当道路横纵坡固定后，由以上公式可求流量、过水断面宽度或水深间的关系，例如：假设道路纵坡为 0.01、横坡为 0.02，、取曼宁系数 n=0.016，设流量Q=0.05 m3/s，则过水断面为：

B=[Qn/（0.377SC1.67Sl0.5）]0.375=[（0.05）（0.016）/0.377×0.021.67×0.010.5）]0.375=2.7（m）

当过水断面宽度B=2.5 m，及水深h为0.05 m时，流量Q为：

Q=0.377×2.52.670.021.67×0.010.5/0.016=0.036（m3/s）

3.2 带低洼区的三角形沟渠流量计算

可定义过水断面宽度B1和B2范围内的流量分别为 Q1、Q2，则：

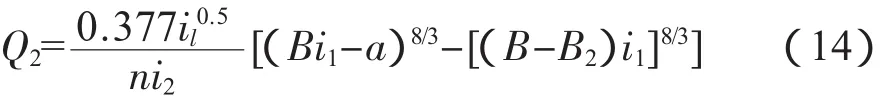
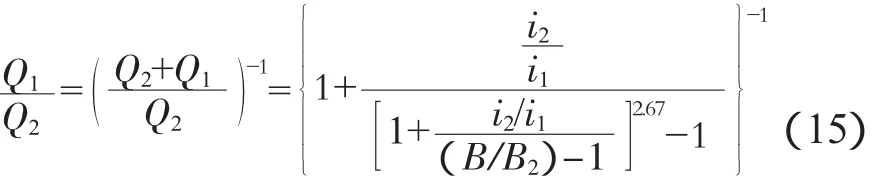
算例：同样假设道路纵坡为0.01、横坡为0.02、过水断面宽度为2.5 m，其中低洼区宽度为0.6 m，深度为50 mm，则：

i2=i1+0.05/0.6=0.103

Q1=0.377×0.010.5×0.021.67×（2.5-0.6）2.67=0.019（m3/s）

Q=Q1+Q2=Q1/（1-0.7）=0.06（m3/s）

由上述计算可看出，增加低洼区后，相同条件下，流量从0.036 m3/s增加至0.06 m3/s，增加了72%，因此，条件允许时，可通过设置低洼区以增大流量，或减小过水断面宽度。

3.3 矩形、梯形边沟流量计算

通过曼宁公式，同样可以解决此问题，过水断面的面积可使用下式表示：

式中：m1、m2——分别代表梯形边沟侧壁的坡比。

湿周的表达式如下：

式（17）中，k为计算系数。对称梯形边沟，k=2 1+m2；不对称梯形边沟，k=2 1+m11+1+m22；矩形边沟，k=2(m=0)。

3.4 半圆形边沟流量计算

流量计算公式可表示为如下形式：

式中：d——半圆形边沟的直径；

n——曼宁系数。

此时过水断面的宽度可由下式计算[4]：

算例：假设管直径为1.5 m、纵坡为0.01、曼宁系数为0.016、流量为0.5 m3/s，则：

过水断面宽度为：B=2[0.752-（0.75-0.3）2]0.5=1.2（m）

由计算分析可知：半圆形沟渠的排水能力较大，相同流量时，过水断面宽度也较小。

3.5 皿型边沟流量计算

其过水断面面积及湿周的计算公式如下：

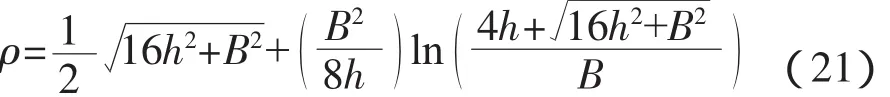
将上两式相除，即可得水力半径，再代入流量计算公式可求沟渠流量。

3.6 V字型沟渠流量计算[5]

V字型沟渠采用双向横坡，横坡采用如下公式计算所得的综合横坡值：

式中：SC1、SC2——分别为V字型边沟的左右两侧侧壁的坡比。

算例：假设两侧壁的坡比分别为0.025、0.04，纵坡为0.01，曼宁系数为0.016，流量为0.05 m3/s，则过水断面宽度计算如下：

SC=（0.25×0.04）/（0.25+0.04）=0.0345

B=[（0.05×0.016）/（0.377×0.03451.67×0.010.5]0.375=1.9（m）

由此可见，加大横坡或采用双向倾斜侧壁可增加流量或减小过水断面的宽度。

3.7 带浅槽的三角形沟渠

如图2，在求出侵入路面的水面宽度B2之后，可按梯形面积公式分别求得浅槽汇水面积和浅槽上部的双向开口且有变坡浅三角形汇水面积两部分 A1，A2。

通过如下的变换，可将带槽的浅三角形沟变换为汇水面积同水深水面宽度B(B1+B2)单坡直立浅三角形沟，其等效水深h*和沟横坡SC*为：

在求得等效水深和沟横坡后，可按三角形沟渠流量计算公式计算流量。

3.8 用于路堑路段的V字型沟渠流量计算

如图3圆弧段两侧宽度B1、B2为：

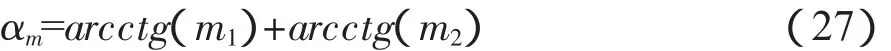
式中：αm——圆弧段的夹角；

m1、m2——V字型边沟两侧边壁的坡比。

若水面未淹过两侧圆弧时，边沟为大尺寸的皿型沟；当水面超过两侧圆弧，可采用下式近似计算其设计流速v和泄水能力Qc：

式中：h*、v*、Qc*——不计圆弧影响的三角形沟的水深、平均流速、泄水能力；

B——水面宽度；

ξ——皿形修正系数，皿形面积A与三角形

面积A*之比值（A/A*）。

此公式是建立在皿形沟湿周用三角形湿周近似替代的前提下的，当m1≥ 6和 m12≥4(高速、一级公路的一般要求)时，湿周ρ的误差不到1.5%，平均流速v和泄水能力Qc的误差分别小于1%和3%。

以上内容即为不同形式沟渠的流量计算方法，矩形及梯形沟渠流量计算较为简单；皿型沟渠流量计算可参阅半圆形沟渠；带浅槽的三角形沟渠可按三角形沟渠计算其流量，因此次几种沟渠的流量计算未给出算例。计算沟渠流量的目的是设计的沟渠尺寸所对应的流量应大于等于设计流量，或以设计流量为依据计算沟渠的最小尺寸。

4 水流在曲线段的流动

沟渠中的水流在曲线段流动时，水流方向会发生改变，且会产生离心力。离心力会使水流外侧的高度高于内侧，即产生超高，如沟渠边壁不做正确设计，则有可能会出现水流溢出沟渠边界的可能。此超高可由下式进行计算：

式中：B——水面宽度，m；

Δh——曲线段流动时沟渠内外侧水流表面的高度差，m；

rc——沟渠中线的半径，m；

g——重力加速度，9.81 m/s2；

其他符号意义同前。

式（31）对缓流是适用的，和沟渠中线的水面高度相比，外侧水面高度要高出Δh/2，而内侧水面要低 Δh/2。

水流为急流时，进入曲线段后，由于由于凹槽壁的阻碍，水流将出现激波，使水面壅高。在进入弯道后的偏转角θ0处水面达到最高，矩形槽的θ0的计算式为：

式中：b——沟渠的宽度；

β1——初始波角，sinβ1=Fr；

其它符号意义同前。

曲线段沿沟渠边壁的水深为：

对外侧边壁，偏转角θ0为正值；对内侧边壁，偏转角θ0为负。

水流为急流时，曲线段内外侧边壁水面最大超高近似为缓流超高的2倍，为，即激波波幅为。

水流进入弯道会出现环流，水头损失增加，从而在弯道的前端水面被抬高Δh。大部分能量消耗在上游段，一小部分消耗在下游段。弯道前端水面抬高量Δh与弯道曲率半径rc、水面宽度B、水深h、转角θ0，以及雷诺数Re有关。其中，弯道曲率半径rc与水面宽度B之比值rc/B影响最大，在rc/B≥3时，水面抬高量Δh较小，可予忽略。

通过以上分析可知，水流在曲线段流动时，由于离心力的作用，会导致外侧水面高于内侧水面的现象，抬高的高度和水流流态有关。在曲线段修建沟渠时，应注意根据计算结果使边沟外侧高于内侧。

5 结语

对排水沟渠的应用，应首先根据道路条件决定其形式，然后计算其流量，使其满足设计流量的要求，从而确定出排水沟渠的尺寸。当计算尺寸过大时，可变换沟渠形式，或减小汇水面积以使尺寸满足要求。

[1]姚祖康.公路排水设计手册（第一版）[M].北京：人民交通出版社，2002.

[2]叶镇国主编.水力学及桥涵水文第一版）[M].北京：人民交通出版社，2003.

[3]李家春.高等级公路路面集中排水水力计算[J].重庆交通学院学报，2002，（12）：54-56.

[4]李志勇，王江帅，李彦伟.道路防排水技术第一版）[M].北京：人民交通出版社，2011.

[5]Federal Highway Administration (FHWA).Urban Drainage Design Manual.Hydraulic Engineering Circular No.22.Second Addition,FHWA-NHI-01-021.Washington,D.C.,August 2001.