大跨越钢管混凝土输电塔顺风向分区风荷载谱识别方法
熊铁华,梁枢果
(武汉大学 土木建筑工程学院,武汉 430072)
风灾是电力线路破坏的首要原因。尤其是近年来随着电压等级的提高,高压、特高压输电线路中的塔高、档距相应增加,输电塔在强风作用下的风毁事故时有发生,并呈现出越来越多的态势。输电线路抗风设计是国内外风工程界长期关注且至今尚未解决的重大研究课题。我国风工程界对输电塔-线体系抗风设计的理论与试验研究始于上世纪九十年代,已在输电塔-线体系动力计算模型与动力特性分析、风荷载模型与风振响应分析方法以及风洞试验、输电塔失效模式等方面有所进展[1-10]。大量文献资料证明[5-7],输电塔横风向振动响应与顺风向相当,甚至比顺风向大。同时塔的扭转振动亦不可忽略。然而,目前输电铁塔抗风设计只考虑了顺风向,而未考虑横风向与扭转等效风荷载,显然,目前输电塔的动力风荷载模型亟待完善。
由于构造上的特殊性,输电塔所受风荷载很难进行测量,而且就测量精度来说,响应量的测量精度比荷载的测量精度要高。因此利用结构的实测响应量来反演结构的动力荷载,是建立输电塔的动力风荷载模型的重要手段。按照结构风工程界普遍认同的观点,在目前条件下,制作精细、满足基本缩尺律的完全气弹模型风洞试验是把握输电塔-线体系在风荷载作用下的实际力学行为的首要且可靠的方法。该方法可以研究多种风速、多种风向角、多种塔型、多种垂跨比导地线与不同塔高间的匹配情况,可以考虑塔线耦联体系效应、气动阻尼效应等,这是其它方法难以做到的。文献[11]利用气弹模型风洞试验测得模型的位移响应,利用单点响应分别识别出输电塔顺、横风向的单荷载谱。到目前为止,还未见利用多点响应来识别分区多条荷载谱的文献。
本文研究对象为一高395 m的大跨越输电塔,下部主材为钢管混凝土,其它部分为薄壁钢管。由于该塔很高,塔的组成材料上下不同,在实际的工作环境中,塔的上部与下部、顺风向与横风向的风荷载动力模型可能不同。基于此设想,本文将模拟风荷载动力模型的识别过程,建立分区风荷载谱识别的方法,并讨论测量精度、测点数量及位置、模态数及风荷载系数等对荷载识别精度的影响。这些工作将为下一步通过气弹模型风洞试验来识别输电塔的风荷载打好基础。
1 结构模型
本文研究的输电塔模型及坐标系见图1。塔高395 m,塔身为正方形,底部根开为70.6 m。8层以下(下部248.9 m)主材为钢管混凝土,其它部分的主材、斜撑、横隔等全部为薄壁钢管。对有限元模型进行分析,可得到结构的固有频率及振型,并且可知,该结构x、y向的动力特性是相同的[12]。将有限元模型沿y向减缩为图1(c)所示的多质点模型,该模型的前3阶固有频率分别为 0.450 Hz、0.702 Hz、1.032 Hz,前 3 阶振型见图2。经比较,多质点模型与有限元模型的动力特性的误差在5%以内,以下将基于多质点模型进行风致响应分析及风荷载识别。
2 分区风荷载作用下风振响应分析
本文将首先计算输电塔在3种风荷载共同作用下的风振响应,然后尝试以某些点的位移响应来识别风荷载谱。
顺风向脉动风荷载为:

式中:μf(z)为脉动系数;μs(z)为体型系数;μz(z)为风压沿高度z变化系数;w0为基本风压;Ar为节点承风面积;f(t)为归一化顺风向脉动风压随机函数。
本文研究的输电塔高395 m,塔的下部又是钢管混凝土,在此设想f(t)沿塔高分布不同,分为3种类型:f1(t),f2(t),f3(t),对应的自功率谱密度分别为 S1,S2,S3。其中S1作用在图1(c)中的1~6号质点(上部66 m区间),S2作用在7~13号质点(中部80.1 m区间),S3作用在14~20号质点(下部248.9 m区间)。本文选择的3种风荷载谱见图3(计算中频率范围为0~5 Hz,为了清晰只显示出 0~1 Hz,下同),其中 S1为Davenport谱,其它两条是人为构造的谱曲线。
设输电塔结构具有n个自由度,每个自由度上均作用有平稳随机风荷载,利用虚拟激励法[13],风荷载矢量表达式为:

图1 有限元及多质点模型Fig.1 Models of FEM and multi-freedom

图2 结构前3阶振型Fig.2 The first 3-order vibration modes of the structure

则风荷载的互功率谱矩阵为:

式中:为简化用aj代替aj(z);*表示取复共轭。
多自由度系统位移频响函数矩阵[H(iω)]中任意元素Hpq(ω)为q点单位激励在p点产生的位移,表达式为:

式中:ωr、ζr分别为结构第 r阶频率、阻尼比;φpr、φqr分别为p、q点在r阶正则化振型中的幅值。
则结构位移响应互功率谱矩阵为:

图4为计算得到的第1、8、14、18号质点的位移自功率谱曲线。

图3 荷载功率谱曲线Fig.3 Load spectra

图4 位移功率谱曲线Fig.4 Displacemental spectra
3 分区风荷载谱识别
设试验中测量得到的是结构的m个位移响应{y},其与结构的总位移向量{Y}的关系为:

其中:[Ey]是{y}对{Y}的提取变换阵,由0、1 组成,且是行满秩矩阵。而这m个测点的位移互功率谱矩阵为:

将式(2)改写为:

其中:[Es]为提取变换阵,由0、1组成,其列数为需识别的荷载谱种类数目。[A]为一对角矩阵。
则风荷载的互功率谱矩阵式(3)可改写为:
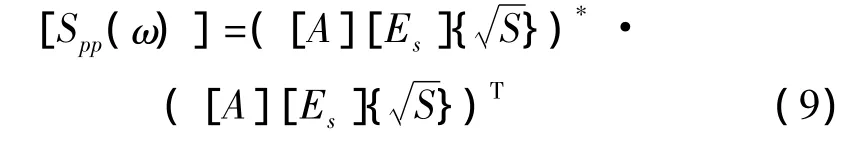
由式(5)、(7)、(9)有:

其中:

因此,只要获得测点的位移互功率谱矩阵,即可由式(10)得到荷载谱矩阵:
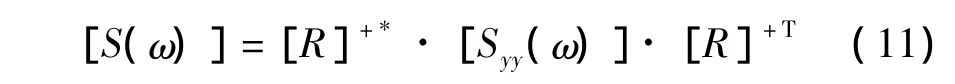
式中,“+”号表示矩阵的广义逆。一般而言,测点数、模态数必须不少于待识别的荷载数,式(11)才有解。
4 荷载谱识别结果分析

4.1 测量精度的影响
将前述风振位移响应计算结果取不同的有效数字,来模拟实际的测量精度。
图5、6分别为表1中工况1、2时荷载识别的结果。可知,取4个测点、5阶模态、测量精度为mm级时,识别的结果是可以接受的;测量精度为cm级时,识别的结果是不能接受的。当测量精度只有cm级时,将模态数从5提高到10时(表1中的工况3),或将测点数量增加到7个同时取10阶模态(表1中的工况4),识别结果仍然是不能接受的。由此可见,测量精度对荷载识别的精度具有决定性的影响,为了保证荷载识别的精度,位移的测量精度应不低于mm级。现在的激光位移计完全可以保证该测量精度。

表1 测量精度的影响Tab.1 The effects of measurement accuracy

图5 测量精度为mm级的识别结果Fig.5 The load spectra identified when measurement accuracy possessed mm level

图6 测量精度为cm级的识别结果Fig.6 The load spectra identified when measurement accuracy possessed cm level
4.2 测点的影响
测点的影响包括测点数目和测点位置的影响。数学上,要式(11)的反问题有解,必须保证测点数不少于需识别的荷载数。本文需识别的荷载数为3,当测点数为3个、模态数取10阶、测量精度为mm级时(表2中的工况1),识别的结果不能接受。对多种3个测点的组合进行的分析都表明,测点的数目需要多于识别的荷载数目才能保证识别的精度。本文需识别3种荷载,因此最少需要4个测点。测点位置的选择对荷载识别的精度也有重要的影响(塔的上部和中部为薄壁钢管构件,下部主材为钢管混凝土构件):表2中工况2为塔身上部取2个测点、中部和下部各取一个测点;表中的工况3为中部取2个测点、上部和下部各取一个测点,从表可见,两种工况的识别精度均较差,分析表明,此时提高模态数也难以提高识别精度。当下部取2个测点、上部和中部各取一个测点时(表2中工况4、表1中工况1与此类似),荷载识别的结果是可以接受的。将测点数目提高到7个,模态数为10时(表2中工况5),对荷载识别的精度影响不大。

表2 测点的影响Tab.2 The effects of measuring points
4.3 模态数的影响
数学上,要式(11)的反问题有解,必须保证模态数不少于需识别的荷载数。本文需识别的荷载数为3,当测点数为4个、模态数取3、4阶、测量精度为mm级时(表3中的工况1、2),识别的结果不能接受,图7为模态数取3阶的识别结果。当模态数取5阶时(表3中的工况3),识别结果较好,当继续提高模态数到10阶时(表3中的工况4),识别精度没有大的变化。
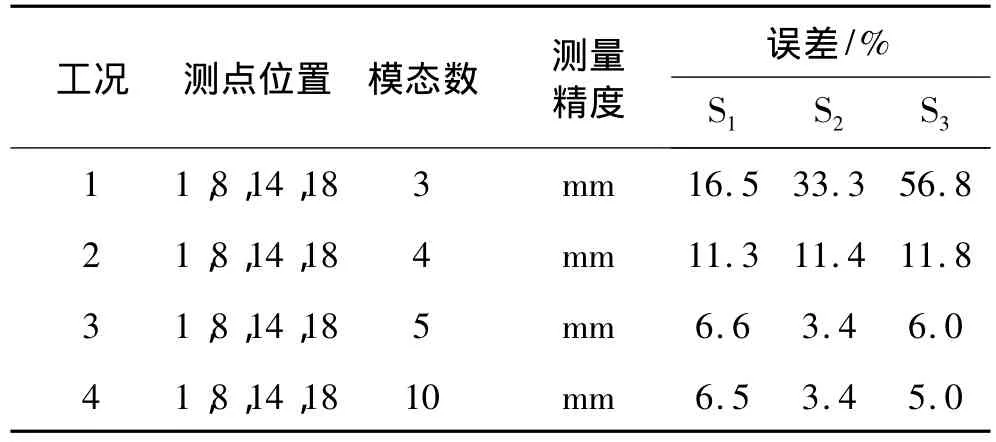
表3 模态数的影响Tab.3 The effects of modes taken
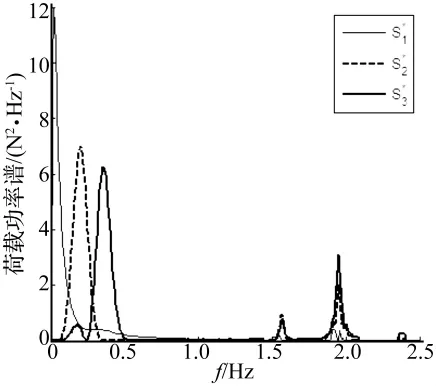
图7 只取前3阶模态的识别结果Fig.7 The load spectra identified when just e first 3-order vibration modes were taken
4.4 风荷载系数a(z)的影响
将式(1)中的a(z)称为风荷载系数。根据气弹模型风洞试验测出位移响应,继而识别风荷载谱时,a(z)中的μs(z)可根据试验确定,而μf(z)、μz(z)需要根据既有文献的统计模型确定,与a(z)有关的其他参数的确定也会存在误差,这样在识别时的风荷载系数a(z)与实际情况往往是不同的。因此,有必要研究风荷载系数对荷载识别精度的影响。
将a(z)看成一个正态分布的随机变量,其均值为a(z),而标准差为 σa(z),σa(z)的取值范围为 0.1 ~0.5倍见表4)。每种工况时,以相应的均值和标准差,按正态分布规律取100个a(z),进行100次荷载识别并有相应的100个识别误差,计算这些误差的均值、标准差。图8为风荷载系数标准差为0.1a(z)时,100次识别中3个荷载谱的误差历程,各历程的均值、标准差见表4中工况1。表4为测点位置取1,8,14,18等4个点,模态数取5阶、测量精度为mm时,荷载系数具有不同标准差的各工况荷载识别误差。由表4可知,随着荷载系数标准差的增大,各工况荷载谱误差均值及误差的标准差也在增大,当风荷载系数标准差控制在其均值30%以下时,荷载识别的结果是可以被接受的;同时也可知荷载识别误差对风荷载系数不是很敏感,这对风荷载的识别是很有利的。

表4 风荷载系数的影响Tab.4 The effects of wind load coefficient

图8 工况1时,荷载谱识别的误差历程Fig.8 Error curves of the load spectra identified in condition 1
5 结论
为了从风洞试验测量的位移响应中较好地识别出钢管混凝土输电塔的风荷载,本文对荷载识别过程进行了模拟。首先选择了3种类型的风荷载谱并将它们分区施加于输电塔的多质点模型上,利用随机振动理论计算出结构的位移功率谱;然后,推导出识别分区风荷载谱的方法,并定义了评价识别效果的误差指标;最后,分析了测量精度、测点数量及位置、模态数及风荷载系数等对荷载识别精度的影响。得到一些对实际风洞试验具有重要指导价值的结论:
(1)测量精度对荷载识别的精度具有决定性的影响,其应达到mm级;
(2)测点的数目和位置、模态数等对荷载识别的精度具有重要影响,它们需要根据具体的结构通过数值模拟来确定;
(3)荷载识别误差对风荷载系数不是很敏感;
(4)完全相关分区风荷载谱是可以被识别出来的,部分相关分区风荷载谱的识别有待进一步研究。
[1]Zou L H,Liang S G,Li Q S,et al.Investigation of 3-D dynamic wind loads on Lattice towers[J].Wind and Structures,2008,11(4):323 -340.
[2]梁枢果,邹良浩,赵 林,等.格构式塔架动力风荷载解析模型[J].同济大学学报(自然科学版),2008,36(2):166-171.LIANG Shu-guo, ZOU Liang-hao, ZHAO Lin, etal.Analytical model of dynamic wind loads on lattice towers[J].Journal of Tongji University:Natural Science,2008,36(2):166-171.
[3]梁枢果,朱继华,王力争.大跨越输电塔-线体系动力特性分析[J].地震工程与工程振动,2003,23(6):63-69.LIANG Shu-guo,ZHU Ji-hua,WANG Li-zheng.Analysis of dynamic characters of electrical transmission tower-line system with a big span [J]. Earthquake Engineering and Engineering Vbration,2003,23(6):63 -69.
[4]梁 波,徐建良.架空输电铁塔动力风响应的数值模拟[J].同济大学学报(自然科学版),2002,30(5):583-587.LIANG Bo,XU Jian-liang.Numerical simulation of alongwind response of transmission towers[J].Journal of Tongji University:Natural Science,2002,30(5):583 -587.
[5]梁枢果.输电塔-导线体系风振响应计算与气弹模型风洞试验研究报告[R].上海:同济大学土木工程防灾国家重点实验室访问学者基金资助项目,2002.
[6]楼文娟,孙炳楠,叶 尹.高耸塔架横风向动力风效应[J].土木工程学报,1999,32(6):67-71.LOU Wen-juan, SUN Bing-nan, YE Yin. Across-wind dynamic response oflatticed towers[J]. China civil Engineering Journal,1999,32(6):67 -71.
[7]梁枢果,邹良浩,赵 林,等.输电塔-线体系完全气弹模型风洞试验研究[J].土木工程学报,2010,43(5):70-78.LIANG Shu-guo,ZOU Liang-hao,ZHAO Lin,et al.Study of wind tunnel tests of a full aero-elastic model of electrical transmission tower-line systems[J].China Civil Engineering Journal,2010,43(5):70 -78.
[8]邓洪洲,朱松晔,陈晓明,等.大跨越输电塔线体系气弹模型风洞试验[J].同济大学学报(自然科学版),2003,31(2):132-137.DENG Hong-zhou,ZHU Song-ye,CHEN Xiao-ming,et al.Wind tunnel investigation on model of long span transmission line system[J].Journal of Tongji University:Natural Science,2003,31(2):132 -137.
[9]熊铁华,梁枢果,邹良浩.风荷载下输电铁塔的失效模式及其极限荷载[J].工程力学,2009,26(12):100-104.XIONG Tie-hua, LIANG Shu-guo, ZOU Liang-hao.Dominant failure modes of a transmission tower and its ultimate capacity under wind load[J].Engeering Mechanics,2009,26(12):100 -104.
[10]熊铁华,梁枢果,邹良浩.考虑断线时输电铁塔的失效模式及其极限荷载[J],土木工程学报,2009,42(11):86-90.XIONG Tie-hua, LIANG Shu-guo, ZOU Liang-hao.Dominant failure modes of transmission towers and the limit loads with wire breakoff[J].China Civil Engineering Journal,2009,42(11):86 -90.
[11]熊铁华,梁枢果,邹良浩.基于完全气弹模型风洞试验输电塔风荷载识别[J].建筑结构学报,2010,31(10):48-54.XIONG Tie-hua,LIANG Shu-guo,ZOU Liang-hao.Wind loading identification of transmission towers based-on wind tunnel tests of full aero-elastic model[J].Journal of Building Structures,2010,31(10):48 -54.
[12]熊铁华,梁枢果,邹良浩,等.大跨越钢管混凝土输电塔线体系的地震响应分析[J].土木工程学报,2010,43(12):7-12.XIONG Tie-hua,LIANG Shu-guo,ZOU Liang-hao,et al.Seismic responses of a long-span concrete filled steel-tube transmission tower-line system [J].China Civil Engineering Journal,2010,43(12):7 -12.
[13]林家浩,张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004.

