雷达目标回波模拟研究与实现

张坤峰，罗 杰

（船舶重工集团公司723所，扬州 225001）

0 引 言

现代雷达技术和电子对抗技术的飞速发展使得战场电磁信号环境日趋复杂，电磁信号密度越来越高。新体制雷达和新型电子战装备的研制生产、调试测试、性能检测和评估鉴定已不能单纯地依赖外场试验，在外场不但无法构建出复杂的电磁信号环境，而且试验成本昂贵。随着现代雷达及电子对抗模拟仿真技术的发展，通过雷达及电子对抗模拟仿真设备可在内场构建逼真的雷达信号、雷达目标回波、雷达干扰信号和通信、导航等信号组成的复杂战场电磁环境，已成为雷达装备和雷达对抗装备性能评估、试验定性和模拟战场训练所关注的焦点。通过内场试验不但可以完成雷达装备的战技性能及其抗干扰能力试验、雷达侦察装备的侦察分选能力试验和雷达干扰装备的干扰效果试验，而且可以进行雷达和雷达对抗装备的战场模拟训练。雷达目标回波模拟技术作为雷达及电子对抗模拟仿真领域的一项重要技术，在内场复杂电磁环境构建中扮演着不可或缺的角色，雷达目标回波模拟的高逼真度是内场构建逼真战场电磁环境的需求。

1 雷达目标回波模拟分析

雷达的最终目的是为了获取雷达目标信息，包括雷达目标的运动与轨迹信息、几何特征和物理参数［1］。为了准确模拟雷达目标回波信号，使雷达装备能够准确获取目标的特征信息，必需模拟雷达目标回波所对应的运动、几何和幅度、闪烁等特征信息。对于具有一定轨迹的运动目标的模拟需建立目标运动航迹模型、目标时延模型和多普勒频移模型，对于几何特征和物理参数需建立目标雷达截面积和幅度起伏模型。当雷达目标处于战场环境中，还需考虑目标的距离衰减、大气衰减等因素，应建立雷达目标回波的功率衰减模型。因此，结合工程实现考虑，需模拟的雷达目标回波特征信息主要包括：

（1）目标运动航迹；

（2）回波时延；

（3）回波多普勒频移；

（4）回波幅度控制模型；

（5）回波截面积及幅度起伏；（6）回波角闪烁模型。

2 仿真模型

2.1 坐标系及坐标转换模型

雷达目标运动航迹的建立和表征首先需建立确定的坐标系，此处选用的坐标系为大地雷达测量坐标系。所谓大地雷达测量坐标系是以雷达天线为坐标原点建立的一个直角坐标系，Z轴为垂直于雷达处的地面，指向天顶，Y轴指向北极，X轴按右手准则指向东，即通常所说的“北天东坐标系”。其坐标变换主要为直角坐标系和极坐标系之间的变换。

以大地雷达测量直角坐标系O－XYZ为基准，将坐标原点O到目标T的方向定义为径距方向，坐标原点O到目标T的距离R定义为斜距；将斜距R在XY面内的投影与OY轴之间的夹角A z（0°～360°）定义为方向角，顺时针方向为正；将斜距R与XY面之间的夹角E l定义为仰角（或高低角），向上为正（范围－90°～90°），即可表征为极坐标系，如图1所示。

图1 大地雷达测量坐标系直角坐标及极坐标系定义

（1）大地雷达测量直角坐标系到极坐标系转换的数学模型如下：

（2）大地雷达测量极坐标系到直角坐标系转换的数学模型如下：

2.2 运动航迹模型

目标航迹模型的建立是在大地雷达测量直角坐标系建立的，主要包括直线运动、圆周运动以及由直线运动和圆周运动组合起来的任意航迹。其数学模型如下：

（1）直线运动：

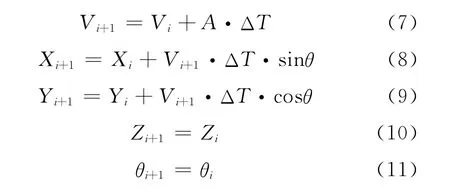
（2）左转圆周运动：

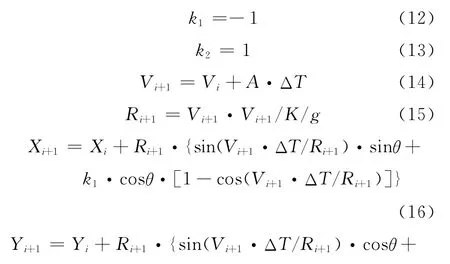
目标航迹模型中的参数定义如下：

V i、Xi，Y i为目标在大地雷达测量直角坐标系的第i次坐标位置（i≥0）；

V i＋1，Xi＋1，Y i＋1为目标在大地雷达测量直角坐标系的第i＋1次坐标位置（i≥0）；

V i，V i＋1为目标在大地雷达测量直角坐标系的第i和i＋1次矢量速度（i≥0）；

θi＋1，θi为目标在大地雷达测量直角坐标系的第i和i＋1次的航向角（i≥0）；

ΔT为目标运动的时间间隔或仿真周期，是第i＋1和第i次时间之差；

A，K，g为目标运动的加速度、机动系数、重力加速度；

k1，k2为目标运动的机动方向控制量。

2.3 回波时延模型

目标回波时延模型建立了当前发射脉冲的回波信号相对当前发射脉冲的时延模型，其数学表述如下：

式中：R为 雷 达 到 目 标 的 距 离，单 位 m；c＝299.79 m／μs，为电磁波传播速度。

2.4 回波多普勒模型

目标回波的多普勒频率模型数学表述如下：

式中：v为目标相对于雷达的径向速度，单位m／s；f为雷达中心工作频率，单位MHz。

2.5 回波功率模型

利用雷达方程可建立单一脉冲雷达目标回波信号的功率模型为：

式中：Pt为被试雷达脉冲发射功率；Gt为被试雷达天线增益；L为被试雷达发射传输损耗；σ为目标雷达平均截面；R为目标至雷达的距离；F为天线方向图传播因子；λ为雷达工作波长；r为电磁波大气传播双程衰减因子。

2.6 回波截面积模型

由于通常目标的形状并不是规则的球体，因此，同一目标在不同方向上的散射能力也不相同，故目标雷达截面就表现出一定的幅度起伏特性和频谱特性。

回波截面积及幅度起伏常采用Swerling模型或用幅度分布和功率频谱分布来描述，其中Swerling模型如表1所示。

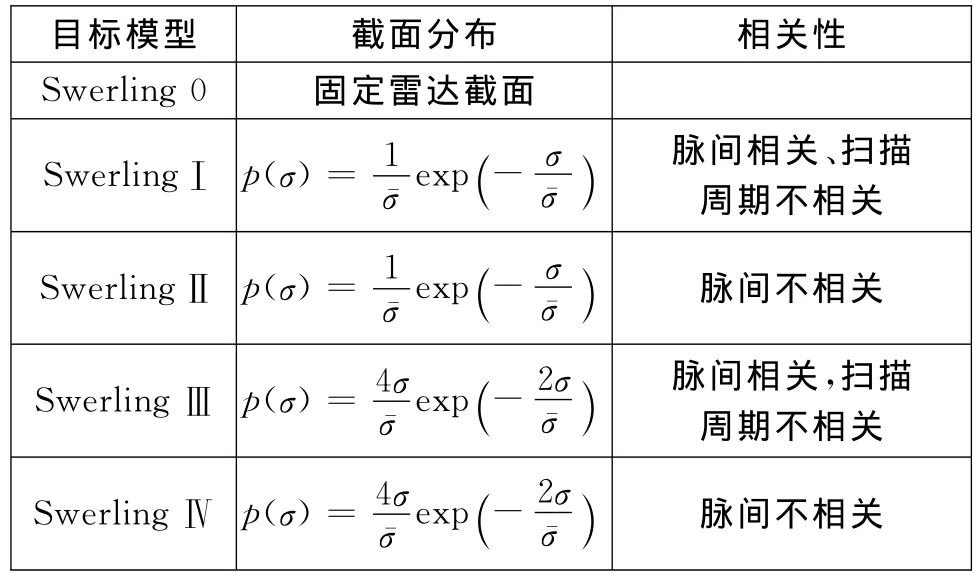
表1 Swerling模型的截面分布和相关性

其中SwerlingⅠ型和SwerlingⅡ型目标RCS的概率密度函数都是指数分布，信号幅度都是瑞利分布，其区别在于SwerlingⅠ型为慢起伏，即从一次扫描到下一次扫描是不相关的，而脉间是相关的；SwerlingⅡ型为快起伏，即脉冲与脉冲间的起伏是统计独立的。SwerlingⅢ型和SwerlingⅣ型目标RCS的概率密度函数为χ2分布，其目标回波的振幅特性为Rice分布，其区别在于SwerlingⅢ型为慢起伏，SwerlingⅣ型为快起伏［2］。

当然也可用特定的幅度分布和功率频谱分布来表征回波截面积，回波的幅度分布可采用生成服从一定幅度分布的随机数作为目标雷达截面的产生，包括对数正态分布、瑞利分布、威布尔分布、K分布；回波的谱分布可采用高斯谱、全极点谱。这些幅度分布和谱分布模型的数学表述可参见《雷达百科全书》，此处不做赘述。

2.7 回波角闪烁模型

角闪烁通常可用正态分布来描述：

式中：σ为角闪烁的均方差，它是目标物理张角的函数。

角闪烁的谱分布仍可用马尔可夫谱描述为：

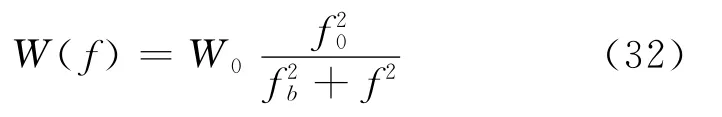
2.8 大气传播衰减模型

在100 MHz～50 GHz频率范围内，大气传播衰减因子可以表示为：

式中：γ1为氧气的衰减因子，以dB／km（双向）为单位；γ2，γ3为水蒸气的衰减因子，单位为dB／km。

在标准温度和标准地面大气压下：

式中：λ为工作波长，以cm为单位；ρ为水蒸气的绝对湿度，单位g／m3，在中纬度地区，缺省值为8 g／m3。

3 系统实现

利用上述仿真模型开发的雷达目标回波模拟系统主要由显示控制计算机、信号处理单元、接收通道单元、下变频网络、上变频网络、频率合成器、宽带数字射频存储器（DRFM）及直接数字频率合成（DDS）单元、射频通道单元等组成。

该系统主要采用了基于宽带DRFM技术、DDS技术、频率合成技术、实时信号处理技术和微波射频技术。其组成原理框图如图2所示。

雷达目标回波模拟系统通过接收天线接收被试雷达的发射信号，经接收通道、下变频网络变为中频信号，由宽带DRFM及DDS单元进行采样存储。显控单元根据战情进行战情解算，向信号处理单元下发战情信息和控制命令，信号处理单元根据目标的位置、速度等信息，解算多普勒频率、距离时延和回波信号幅度起伏，宽带DRFM及DDS单元根据距离时延对采样信号进行恢复，并进行多普勒频率调制，经上变频网络变为射频信号，最后进行幅度控制后，经发射天线辐射出去，模拟产生雷达目标回波信号。

图2 雷达目标回波模拟系统组成原理框图

4 实现效果

利用上述仿真模型和方法实现的雷达目标回波模拟系统在实验室进行测试，得到的目标回波频谱如图3所示；与某型实体装备进行了对接，在雷达显示屏上得出的结果如图4所示。

由此可知，利用上述仿真模型和方法实现的雷达目标回波模拟系统可较好地为实体雷达装备模拟回波信号。

5 结束语

通过对雷达目标回波模拟的简要分析，建立了目标回波模拟所需的航迹模型、时延模型、多普勒模型、幅度起伏模型和角闪烁模型等仿真模型，以及采用上述仿真模型和基于宽带DRFM技术、DDS技术、频率合成技术、实时信号处理技术和微波射频技术实现的雷达目标回波模拟系统，给出了模拟的效果图，取得了较好的模拟效果，对雷达目标回波模拟具有一定的参考价值。

图3 目标回波频谱

图4 雷达显示屏观测的目标回波

［1］黄培康.雷达目标特性［M］.北京：电子工业出版社，2006.

［2］郑灼洋，纪要，罗杰，等.一种相参雷达评估系统的设计及实现［J］.舰船电子对抗，2011（3）：93－96.