基于VC＋＋6.0的激光干涉仪PGC实时检测解调算法优化

金天星

（船舶重工集团公司723所，扬州 225001）

0 引 言

近年来，随着潜艇消噪技术的不断提高，低噪声潜艇的辐射噪声已接近于海洋环境噪声，迫切需要研制灵敏度极高的探测器对其进行探测。而激光干涉仪测量法在测量低频微小振动中具有测试灵敏度高、精度高、频率范围广、电气绝缘、不会引起电网谐振等优点，是实现高精度振动测量的主要方法之一。在这种背景下，基于激光干涉原理对潜艇进行探测成为未来主要研究方向之一。在激光干涉测量系统中，解调单元对激光干涉测量的精确度、分辨率和动态性能指标有重要的影响。解调方法的选择是整个解调单元算法的核心，而相位载波（PGC）解调法是一种开环检测方案，它利用远离信号频带的高频、大幅度载波信号对激光干涉仪的初始相位进行调制，减少由于相位随机漂移对信号检测灵敏度的影响，通过信号处理将声信号从载波信号中提取出来。PGC检测法是到目前为止激光干涉仪诸多解调算法中应用最广的一种算法。

1 PGC检测原理

激光干涉仪采用迈克尔逊激光干涉仪，干涉后的光信号经光电转换后可以写成［1］：

式中：A为干涉仪输出的平均光功率；B＝κA，κ≤1为干涉条纹可见度；Φ（t）为干涉仪两臂间的相位差，设Φ（t）＝Ccosω0t＋φ（t），则式（1）可写为：

式中：Ccosω0t为相位载波；φ（t）＝Dcosωs（t）＋Ψ（t），Dcosωs（t）为待测信号引起的相位变化，Ψ（t）为环境扰动等引起的初始相位的缓慢变化。

将式（2）用Besssel函数展开，得：

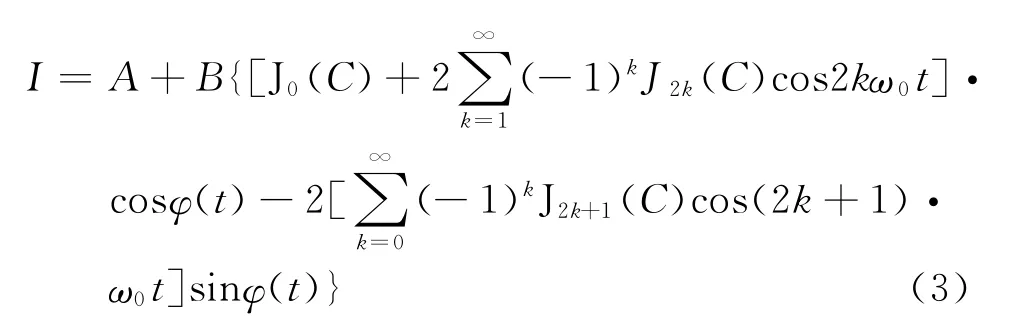
图1为PGC解调总体方案框图，将余弦信号Gcosω0t和Hcos2ω0t分别与干涉仪的输出信号I混频，并通过低通滤波器（LPF）得到－BGJ1（C）·sinφ（t）－BGJ2（C）cosφ（t），然后，采用微分交叉相乘（DCM）技术，可得B2GHJ1（C）J2（C）φ（t）。

积分运算处理后，可得B2GHJ1（C）J2（C）［Dcosωst＋ψ（t）］。可见，积分后得到的信号包含了待测信号和外界的环境信息，后者通常为慢变信号，通过高通滤波器滤除，系统的最后输出为：B2GHJ1（C）J2（C）Dcosωst。

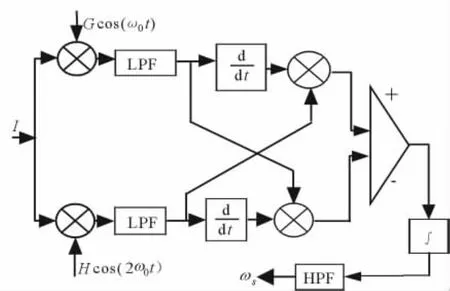
图1 PGC信号解调总体方案框图

2 PGC解调中的多线程技术

本次实验主要是基于上位机的解决方案。上位机的VC＋＋应用程序主要是负责对采集到的数字信号进行存储和解调，并且将采集、解调处理后的信号实时显示出来。

由于此次实验具有实时性的要求，所以本VC＋＋程序采用多线程思想，一个线程负责数据采集和存储，另一个线程负责数据处理及显示，加上本个人计算机（PC）机具有双核配置，这样能很好地利用PC机上多中央处理器（CPU）的性能，使实时性能进一步提高，基本可以满足实验要求。

上位机采用 Windows操作系统，Windows函数库中提供现成的多线程函数，对多线程的创建等非常方便，线程创建的函数如下［2］：

本次实验中，2个线程之间需进行数据交互，需同时访问采集的数据。这时如不进行冲突控制的话，很可能显示的是不正确的结果。对共享资源进行访问引起冲突是不可避免的，但是采用线程间同步技术可以较好地解决资源共享冲突的问题。

线程间同步经常采用的方法有建立互斥对象、设置信号、事件对象和设置排斥区的方法，本程序采用的则是设置排斥区的方法。设置排斥区的方法具有交互性能好、操作实现简单的优点。

3 PGC算法优化

实验对数据处理、显示的实时性要求很高，尤其对于用上位机进行数据解调来讲，实时性的要求就更高。由于地声信号一般都是几十Hz的低频信号，而信号载波频率相对于要解调的地声信号来讲，频率比较高，所以对于频率分辨率的要求也比较高。为了提高频率分辨率，就要求每次处理的数据点要尽量大，这样经过傅里叶变换以后，频谱的分辨率也会相应提高，以满足实验要求。

但这样一来，需要处理的数据量也会很大，同时高采样率对处理时间的要求也比较高。在PGC算法中，由于涉及到高通、低通滤波器，加大了数据处理的运算量，对CPU要求更高，对整个系统增加了运行时间，对系统的实时性影响很大。

在程序实现中，由于C语言具有良好的执行速度和灵活的编程方法，所以用C语言作为编程语言可以很好地满足要求。下面从3个方面对PGC算法进行优化［3－5］。

3.1 数字滤波器的优化

在相位解调算法中，数字滤波器的运算量占据了很大一部分，每次算法实现过程包含了2次低通和1次高通。但是为了达到解调后的精度，滤波器的精度是不允许降低的，所以对滤波算法的优化就显得很有必要。

对于数字滤波器的实现，包含无限冲击响应（IIR）滤波器和线性相位的有限冲击响应（FIR）滤波器。本次实验中相位解调算法对于信号相位要求非常严格，所以程序中选用FIR滤波器。FIR滤波器不像IIR滤波器那样有完整的设计公式，只能借助计算机辅助设计进行滤波器系数的求解。

这里选择Matlab进行滤波器系数的求解，使用简单方便，将Matlab中求解的滤波器系数导入VC＋＋中，可以进行直接运算，简化了求解过程。以汉明窗、阶数是25阶、采样频率与截止频率分别为100 000 Hz和5 000 Hz的低通滤波器为例，Matlab求解FIR滤波器系数的程序如下：

线性相位滤波器具有系数对称的特性。对于1个8阶的FIR滤波器来讲，传递函数如下：

若直接运算，总共需8次乘法和7次加法。如果改写成：

可看出，只需4次乘法和3次加法。而乘法运算在C语言指令集中占用CPU的机器周期比加法运算要多得多，所以经优化之后，可以减少大量运算。

3.2 数字积分器的优化

由数值分析可知，数字积分算法是要研究如何由函数f（x）在［a，b］区间上若干个点的已知函数值，去计算积分的近似值。一般最为常见的近似方法是梯形公式，即用直线在区间［a，b］上的积分来近似代替f（x）的积分，如图2所示。可得：

从图形上来讲，梯形ABCD的面积近似等于曲边梯形ABCD的面积。

图2 梯形近似法

采用梯形截断法，实际的积分运算是由下面的累加运算近似完成的：

式中：y（n）为当前累加值；y（n－1）为上一次累加值；x（n），x（n－1）为当前采样值和上一次采样值。

但是如果积分不采用梯形近似，而是采用复化梯形公式近似，即将［a，b］进行M等分，得（其中x＝0a，x M＝b）的每个区间，应用梯形公式并累加得：

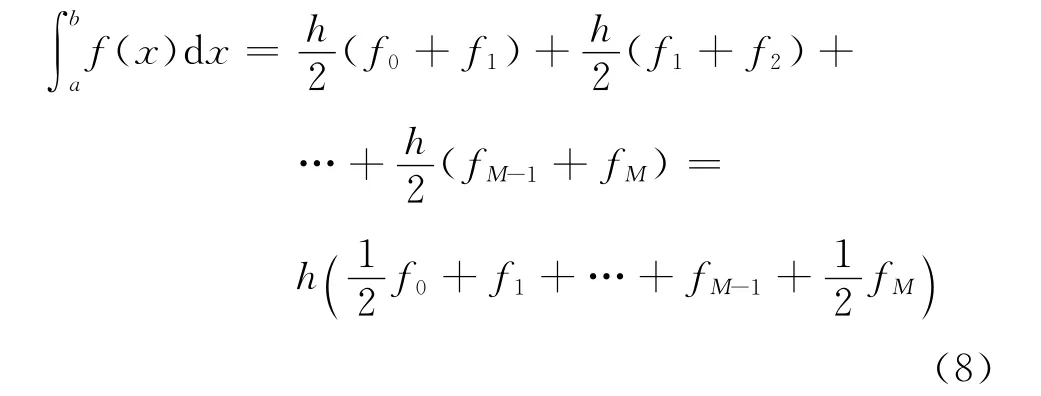
由上述公式变形后的数字化解调系统中的积分算法为：

可见使用复化梯形公式计算后，减少了计算量。

3.3 降采样算法研究

由图1所示的PGC解调方案可知，经低通滤波后，待检测信号的频率远小于采样频率。根据降采样原理，可对信号进行降采样处理，以降采样N倍为例，即是对滤波后的数据每隔N－1个数据进行数据的再次抽取。降采样后系统采样率变为原来采样率的1／N倍，但在降采样的过程中，不能忽略奈奎斯特采样定理，即原来的采样率至少是N倍的奈奎斯特频率。经降采样之后，大大降低了每次运算时数据量的长度。根据相位解调算法，在高通滤波和积分运算之间还可以进行1次降采样处理。这个阶段的信号都是低频信号，而这些信号的频率远远低于采样率。同时为了提取待检测信号，需要进行高通滤波。因为外界缓变信号的频率往往低于5 Hz，如果截止频率为5 Hz，又是高采样频率的话，高通滤波器的阶数将非常大，不利于系统实时性的实现。

4 结束语

本文阐述了PGC相位检测技术的原理以及在VC＋＋下运用多线程进行编程的方法，并且详细介绍了在VC＋＋平台下PGC算法的优化问题。由于PGC算法部分对整个程序的运行时间有很大影响，尤其是在较高的采样率时，数据运算量比较大，所以对PGC关键算法的优化很有必要。

［1］田芊，廖延虎，孙利群.光学工程［M］.北京：清华大学出版社，2006.

［2］孙鑫，余安萍.VC＋＋深入详解［M］.北京：电子工业出版社，2006.

［3］张小虹.数字信号处理［M］.北京：机械工业出版社，2005.

［4］刘云涛，曹家年，李丁山，等.基于PGC解调方案的时分复用光纤传感器阵列采样频率的研究［J］.哈尔滨工程大学学报，2001，22（6）：36－40.

［5］万迪，杨军.数字式有源零差激光干涉仪的解调方法研究［D］.哈尔滨：哈尔滨工程大学，2008.