从一道调研试题谈起
——兼谈力学中动态平衡的处理

任汉峰

(江阴市第一中学 江苏 无锡 214400)

下面是一调研试题的原题，笔者将用几种解题方法，对该题做仔细的分析.

【题目】如图1所示，xpy为直角支架，杆xp、绳ao均水平，绳bo与水平方向夹角为60°．如果在竖直平面内使支架沿顺时针缓慢转动至杆yp成水平，且始终保持ao，bo两绳间的夹角120°不变．在转动过程中，设绳ao的拉力Fa、绳bo的拉力Fb，则下面说法中不正确的是

A.Fa先减小后增大

B.Fa先增大后减小

C.Fb逐渐减小

D.Fb最终变为零

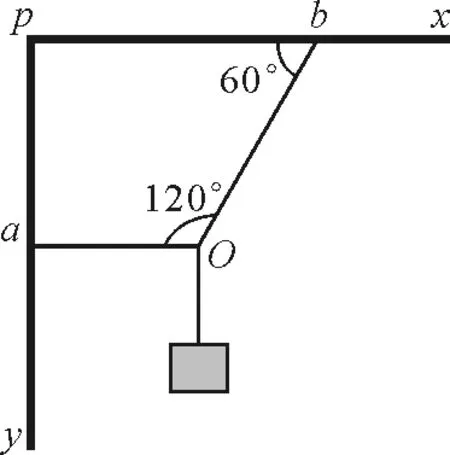
图1

1 正交分解结合函数解析法

解析：假设支架沿顺时针缓慢转过θ，如图2所示，建立水平方向与竖直方向的直角坐标系，然后对接点O进行受力分析，按水平方向与竖直方向进行正交分解，然后列平衡方程

联立平衡方程得

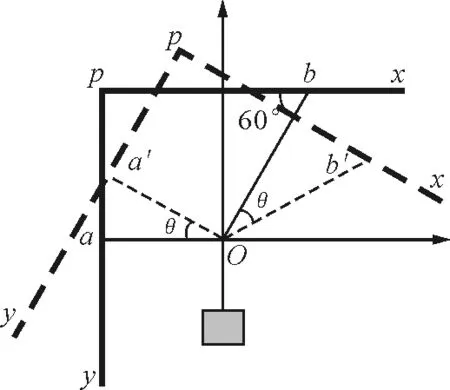
图2

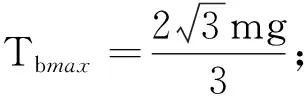
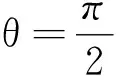
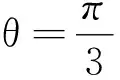
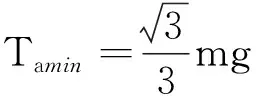
故正确答案为A．

点评：正交分解结合函数解析法是处理力学动态平衡问题中常用方法之一，关键之处在于建立直角坐标系，对研究对象进行受力分析，列平衡方程，得到所研究物理量的函数表达式，然后通过题设中某变化量(如此题中的θ)的变化情况，结合函数来确定所研究物理量的变化情况．正交分解法结合函数解析法可能会对学生的数学能力要求较高，但可能对学生物理思维的能力要求相对要低，换句话说，学生可能容易想到此方法．

2 正弦定理法

解析：假设支架沿顺时针缓慢转过任意角度θ，对结点O进行受力分析，并构建以重力G、绳子拉力Ta、绳子拉力Tb为三角形三边的矢量三角形，并设角度α，β，如图3所示.

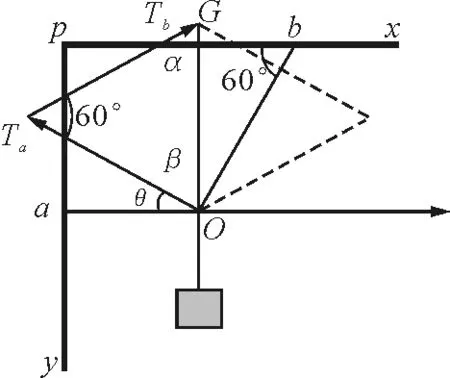
图3

在矢量三角形中，利用正弦定理列关系式

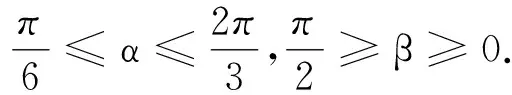
得

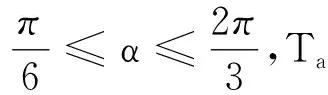
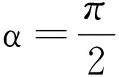
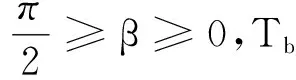
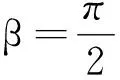
当β=0时，Tbmin=0.

故正确答案为A．

点评：正弦定理法是处理力学动态平衡问题中的方法之一，关键之处在于对研究对象的准确受力分析，构造出与所要研究物理量有关的矢量三角形，并要求准确判断出矢量三角形中关键角度(α，β)的变化范围，利用相应的力与力所对应角度的正弦之比为定值的规律列出关系式，然后通过关键角的变化情况来确定所要研究物理量的变化情况，正弦定理法对学生的思维能力要求较高，学生不容易想到此方法．

3 图解法

解析：结点O受到三个力，其中一绳子拉力T=G，大小与方向均不变，另两绳子在保持夹角120°不变的情况下，大小与方向均在变化，于是，利用转换思维，假设绳子Oa，Ob的拉力方向均不变，T=G的绳子拉力以逆时针缓慢转动，构建以O为圆心，T=G为半径的圆，然后通过图解法作平行四边形，通过平行四边形的两邻边长度的长短来确定Oa，Ob中拉力大小的变化情况，作三组平行四边形，如图4所示，Oa，Ob中拉力大小分别为Ta1，Ta2，Ta3，Tb1，Tb2，Tb3，其中在第三组特殊的平行四边形里，对角线T=G与拉力Ta在同一直线上(最终状态)，即Ta3=T=G，Tb3=0，较容易地从图示中读出Oa，Ob中绳子拉力的变化情况为，Ta先增大后减小，Tb一直在减小．故正确答案为A．

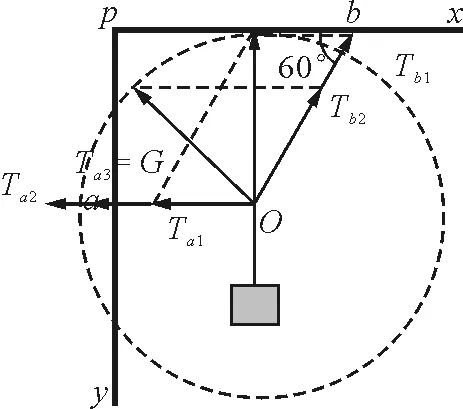
图4

点评：图解法是处理力学动态平衡问题中常用方法之一，关键之处在于准确判断出受力对象的受力特点，一般情况下是受到三个力，其中一个力的大小与方向均不变(通常是重力G或与重力的平衡力)，另一个力的方向不变，第三个力的方向在变，而此题中也是其中一拉力T=G大小方向均不变，另两力方向夹角不变，采用了逆向思维，转换成Oa，Ob两绳子拉力方向不变，T=G大小不变，方向以O圆心逆时针缓慢转动的物理情境，于是问题便迎刃而解，Oa，Ob绳子的拉力变化情况便可直观地从图示中直观地反映出来．图解法在平时的处理问题中，如果掌握了此方法的适用条件后，对学生的思维能力要求应该是较低的，但在处理该题中，还牵涉到了逆向思维的转化法，可能对学生的思维能力要求较高，但也不失为一种好方法．

4 构造圆法

解析：题设中由于绳子Oa，Ob的拉力方向时刻放生变化，而夹角不变，给本题解答带来一定的困难，同时也给此题赋予了一定的创新．鉴于变化过程中绳子Oa，Ob的夹角不变，亦即图5中的60°角度不变，联想到了数学中同一弦(或者圆弧)所对应的圆周角不变，而初始状态正好构建出直角三角形，于是以初始状态下的Tb1为直径，构建出圆，然后在圆中作出特殊的三对矢量三角形，便可从图中直观地反映出绳子Oa，Ob拉力大小的变化，Oa绳子拉力从Ta1变化到Ta2(恰为直径，最大)再到Ta3，先增大后减小；Ob绳子拉力从Tb1(恰为直径，最大)变化到Tb2再到Tb3，一直在减小．故正确答案为A．

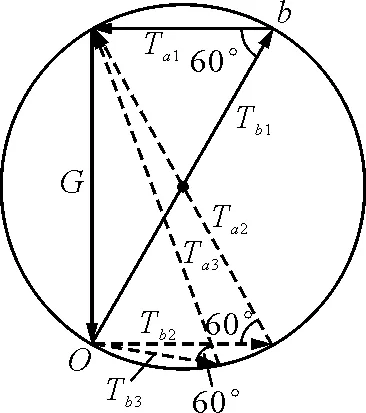
图5

点评：构造圆法在处理力学动态平衡问题中是一种较特殊的方法，关键之处在于发现研究对象的受力特点及其中两个力的夹角始终不变(此题中Ta，Tb夹角不变)，然后通过夹角不变要联想到圆，利用圆的特点，同弦或同圆弧所对应的圆周角相等，在圆中构建出矢量三角形，便可直观地反映出力的变化情况．此种方法对于学生的思维能力要求较高，学生很不容易想到．

5 相似三角形法

【例1】如图6(a)所示，固定在水平面上的光滑半球，球心O的正上方固定一个小定滑轮，细绳一端拴一小球，小球置于半球面上的A点，另一端绕过定滑轮．今缓慢拉绳使小球从A点滑向半球顶点(未到顶点)，则此过程中，小球对半球的压力大小N及细绳的拉力T大小的变化情况是

A.N变大，T变大

B.N变小，T变大

C.N不变，T变小

D.N变大，T变小

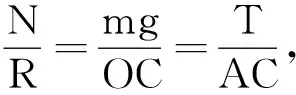
图6

点评：相似三角形法是处理力学动态平衡问题的常用方法之一，关键之处在于准确判断出相似三角形法的适用条件，研究对象受到三个力，其中一个力的大小方向均不变，通常情况下是重力G，另两力的方向均在变化，但是还有隐含的条件：题设中出现边的特点．相似三角形法对学生的能力要求一般，学生很容易联想到此方法．

6 整体法与隔离法

【例2】如图7(a)所示，一个直角支架AOB，AO水平放置，表面粗糙，OB竖直向下，表面光滑，AO上套有小环P，OB上套有小环Q，两环的质量均为m，两环间由一根质量不计、不可伸长的细绳相连，并在某一位置平衡，现将P环向左移一小段距离，两环再次达到平衡，那么将移动后的平衡状态和原来的平衡状态比较，AO杆对P环的支持力FN和细绳上的拉力T的变化情况是

A．FN不变，f变大

B．FN不变，f变小

C．FN变大，f变大

D．FN变大，f变小

图7

解析：如图7(b)所示，P,Q在移动前后的两个状态下都处于平衡状态．设∠OPQ=θ，对整体P,Q：在竖直方向上：FN=2mg，前后FN保持不变．

对Q：Tsinθ=mgθ↑→T↓

对P：f静=TcosθT↓、cosθ↓→f静↓

故正确答案为B．

点评：整体法与隔离法是处理力学动态平衡问题的常用方法之一，关键在于怎么联想到用整体法与隔离法，怎么会发现用整体法与隔离法．那就需要明确整体法的优点：只需分析整体所受的外力情况，回避了整体内部繁杂的相互作用，给解决物理问题带来了极大的方便，但如果需研究内力情况的话，必须采用隔离法，对整体中的其中某个对象进行研究，当然在进行具体受力分析时会选择受力比较简单的．在具体处理问题过程中，整体法与隔离法经常交叉使用．整体法与隔离法对学生的思维能力要求不高，学生也容易想到．

综上所述，介绍了几种处理力学动态平衡问题的研究方法，可能还远不止上述所提，这里不再一一列举．力学动态平衡问题是高中物理教学中的一个难点，也是高考物理的一个热点．因为它涉及到物体受力分析、物体受力处理、解题方法选择等多方面的问题．教师在教学过程中，要让学生在解题过程中多分析，多总结，尝试从不同的题型中归纳出不同的处理方法，这样才能有效提高教学效率，从中培养学生的思维能力，提高学生的解题能力．

物理专题研修