浅谈数学图像在物理中的应用
文棋
(徐州高级中学 江苏 徐州 221009)
众所周知,数学与物理联系紧密,数学是基础,是解题工具.高考物理在考查知识的同时,更注重考查能力,其中很重要的一条就是应用数学处理物理问题的能力.《2011年江苏省普通高中学业水平测试(选修科目)说明》中明确指出:“能够根据具本问题找出物理量之间的数学关系,根据数学的特点、规律进行推导、求解和合理外推,并根据结果作出物理判断,进行物理解释或得出物理结论.能根据物理问题的实际情况和所给条件,恰当运用几何图形、函数图像等形式和方法进行分析、表达.能够从所给图像通过分析找出其所表示的物理内容,用于分析和解决物理问题.”[1]“匀变速直线运动的研究”是高中物理必修的第二章(人教版),本章概念、公式较多,对于刚进入高中的学生而言理解较困难.教师如果能巧妙地结合数学图像讲解、证明本章公式,学生理解起来就较为简单,提高了教与学的效率,达到了事半功倍的效果.下面介绍几个案例(在学生已经掌握了v-t图像,图像与时间轴围成图形的面积即位移大小的知识前提下).
求证1:S第(n+1)T-S第nT=aT2

图1
证明1:如图1,过B1做水平辅助线A2C2,矩形AA2B1B与BB1C2C面积相等,可见梯形BB1C1C比梯形AA1B1B多两个△B1C1C2的面积.
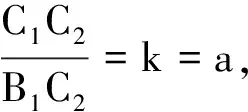
C1C2=aT
2S△B1C1C2=aT2
得证.


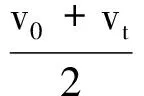

图2
求证3:从静止开始的匀加速直线运动,从初始时刻开始计时,则
v第1T∶v第2T∶v第3T= 1 ∶ 2 ∶ 3
S第1T∶S第2T∶S第3T= 1 ∶ 3 ∶ 5
S前1T∶S前2T∶S前3T= 1 ∶ 4 ∶ 9
证明3:如图3,其中所有小三角形均全等.

图3
v第1T,v第2T,v第3T依次为1个、2个、3个小三角形的高,故
v第1T∶v第2T∶v第3T=1 ∶ 2 ∶ 3
S第1T,S第2T,S第3T依次为1个、3个、5个小三角形面积的和,故
S第1T∶S第2T∶S第3T=1 ∶ 3 ∶ 5
S前1T,S前2T,S前3T依次为1个、4个、9个小三角形面积的和,故
S前1T∶S前2T∶S前3T=1 ∶ 4 ∶ 9
得证.
求证4:从静止开始匀加速直线运动,从初始位置开始计时,经过连续相等位移L时间比为
证明4:如图4,△OAA1与梯形AA1B1B,BB1C1C面积相等,均为L,△OAA1∽△OBB1∽△OCC1.
S△OAA1∶S△OBB1∶S△OCC1=
L∶ 2L∶ 3L=1 ∶ 2 ∶ 3(相似比)
则
所以
OA∶AB∶BC=
t第1L∶t第2L∶t第3L
得证.

图4
综上所述,巧妙地使用数学工具解决物理问题,不仅能激发学生学习物理的兴趣,使学生牢固掌握物理知识,打造高效课堂,还能逐步提高学生应用数学处理物理问题的能力.物理教师应在平时的教学中多思考,多总结,帮助学生跨过一道道思维的“障碍栏”,使学生在物理学习的道路上阔步前进.

