近场动目标多普勒频率、距离及方位估计算法

杨 勇 谭 渊 张晓发 袁乃昌

(国防科技大学电子科学与工程学院微波中心，湖南 长沙 410073)

1. 引 言

空间谱估计是阵列信号处理最主要的两个研究方向之一，侧重于研究空间多传感器阵列所构成的处理系统对感兴趣的空间信号的参数进行准确估计的能力，其主要目的是估计信号的空域参数或信源位置[1]。在远场信源的条件下，信号波前为平面波，信源位置可以直接由空间谱即信号的波达方向(DOA)得到。但在近场情况下，信号波前为球面波，信源位置需由距离及DOA联合确定。

近年来，针对近场源的定位，已提出了很多算法。文献[2]将一维MUSIC推广到二维MUSIC得到距离及DOA的精确估计，文献[3]-[5]提出了基于四阶累积量的近场源频率、距离及到达角估计算法，文献[6]通过构造平行因子模型，然后分解该模型计算得到近场源的三维参数，后面两类算法计算量较二维MUSIC小而且不需谱峰搜索，但其只能在阵列为均匀阵的条件下适用，而MUSIC算法[7- 8]可用于任意阵列。

以上的算法均讨论的是被动近场源的定位，同时，算法能分辨的信源数小于阵元数目。这里提出一种主动式近场动目标的参数估计算法，用于近场具有不同运动速度的多动目标定位。根据各目标回波信号对应多普勒频率的不同，首先采用一维MUSIC算法估计信号频率并进行时域滤波，将各目标对应信号加以分离，然后由二维MUSIC算法估计各目标的距离及方位。该算法能精确地对近场动目标进行定位，同时其可分辨目标数不受阵元数限制。

2. 信号模型

假设K个动目标位于M元直线阵列近场(如图 1)，采用宽波束天线发射频率为f0的毫米波连续波信号，直线阵列天线接收，为保证估计精度并减小系统复杂度，阵元位置可采用遗传算法优化稀疏排列[9-11]。设阵元位于x轴上，其x坐标为x1,x2,…,xM，各动目标回波信号多普勒频率各不相同且对于各阵元多普勒频率近似相等。将接收信号混频到中频fI，以原点O的相位为参考，则第m个阵元接收信号可表示为

(1)

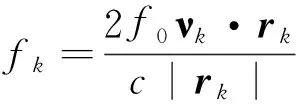
(2)

其中：rk为目标k到原点的距离；c为光速。

以采样频率fs对接收信号进行采样并将其分为N个数据块，第n个数据块从tn时刻开始取L次快拍，则接收信号可用M×L维矩阵表示

X(n)=AS(n)GH+N(n)

(3)

式中：X(n)=[x(tn) …x(tn+(L-1)/fs)]；A=[a(r1,θ1)a(r2,θ2)…a(rK,θK)]为M×K维阵列导向矩阵;S(n)=diag{s(tn)}为信号幅度矩阵，s(tn)=[s1(tn)…sK(tn)]T；N(n)为噪声矩阵；G=[g(fI+f1)…g(fI+fK)]为信号矩阵，信号向量可表示为g(f)=[1 ej2πf/fs…ej2π(L-1)f/fs]T.

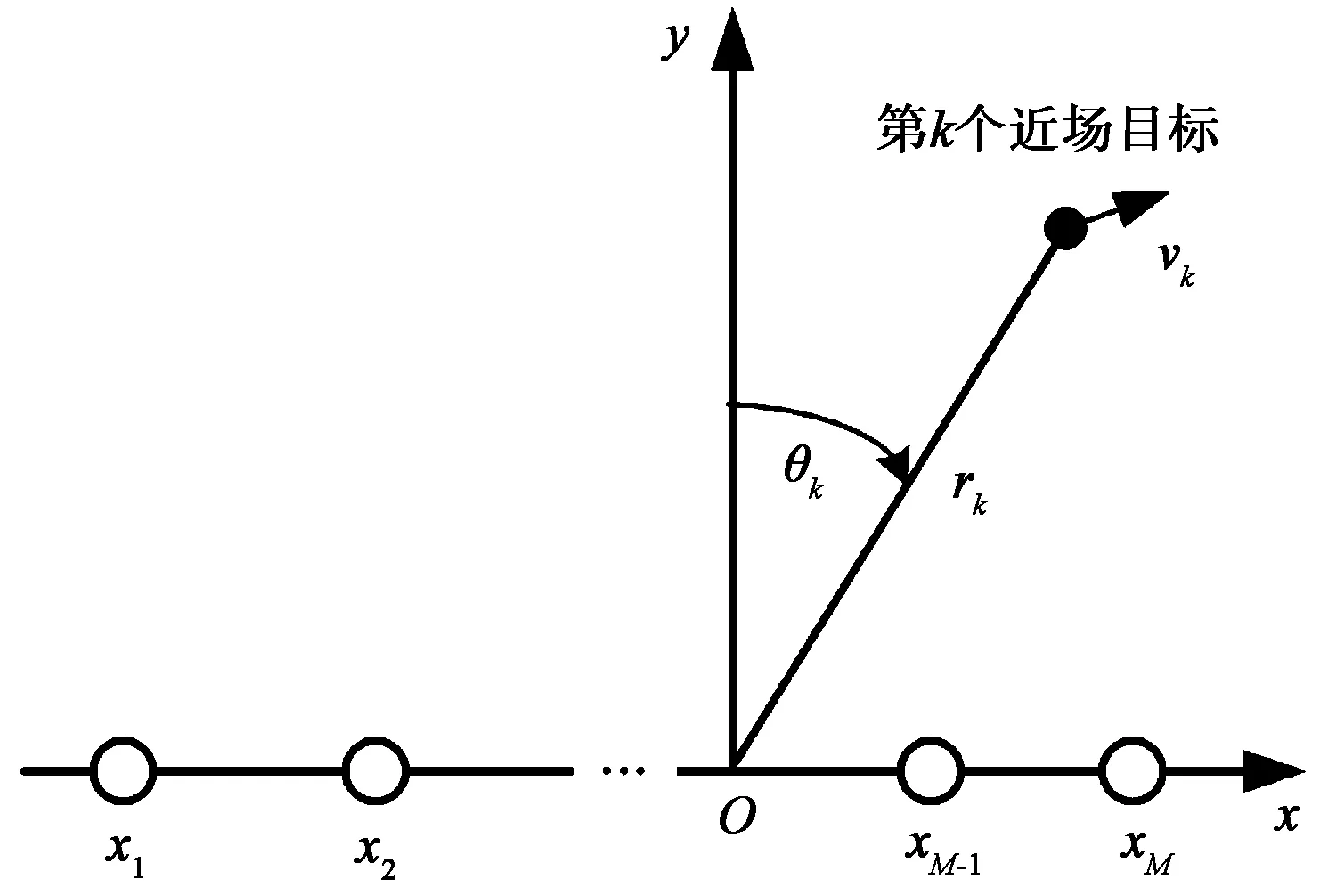
图1 近场目标直线阵列示意图

3. 目标参数估计

为说明算法原理，这里假设了各点目标多普勒频率各不相同且各阵元接收信号的多普勒频率近似相等，阵元噪声为零均值高斯白噪声且与信号统计独立。

3.1 信号频率估计

通过估计接收信号多普勒频率可以分辨不同的目标。考虑信号时间协方差矩阵Rt

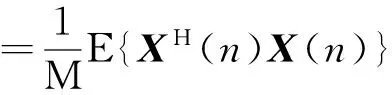
(4)

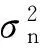
利用等式aH(r,θ)a(r,θ)=M，则上式可化简为

(5)

式中，Rs=E{SH(n)S(n)}。对Rt进行特征分解有

(6)

Uts为信号特征值对应的特征矢量张成的子空间也即信号子空间；Utn为噪声特征值对应的特征矢量张成的子空间也即噪声子空间；Σts，Σtn分别为信号与噪声对应的特征值。

根据信号子空间与噪声子空间正交的性质构造频谱[7]

(7)

`3.2距离与方位估计

根据估计所得的信号频率，可经时域滤波将各目标对应回波信号按不同频率加以分离，然后分别进行处理。这里采用矩阵投影将接收信号投影到各目标对应的频率上，进而采用二维MUSIC算法估计目标的距离和方位。

(8)

式中：

(9)

Np为非负整数，Δ为频谱搜索时的搜索间隔。因频率估计有误差，适当选取Np使得Gk完全包含目标k对应的多普勒频率。将接收数据矩阵乘以投影矩阵得目标k对应信号

(10)

k=1，…，K

式中：Ak=a(rk，θk)为目标k对应的导向矢量；Gk=g(fk)；Sk(n)=sk(tn).因此，接收数据矩阵乘以投影矩阵相当于对接收信号进行滤波。接收信号被滤波为K部分，分别对应K个目标，通过对每部分的数据进行处理得到目标的距离与方位估计。

信号矩阵Xk(n)的协方差矩阵为

(11)

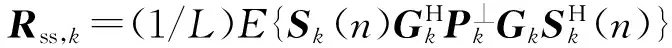
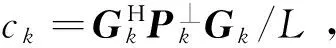
(12)

(13)

即噪声经投影映射后仍为高斯白噪声。对Rs，k进行特征分解

(14)

式中：Vss，k与Vsn，k分别为信号与噪声特征值对应的特征向量，构造空间谱

(15)

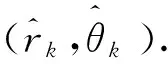
综上，近场动目标多普勒频率、距离与方位估计算法步骤如下：

1) 多普勒频率估计：由接收信号估计信号时间协方差矩阵

(16)

3) 距离与方位估计：对每个Xk(n)，估计其空间协方差矩阵

(17)

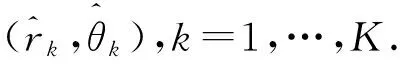
4. 仿真计算

令一维直线阵阵元数为16，阵列孔径为2 m，为避免出现角度模糊，各阵元随机排列。采用宽波束天线发射频率为35 GHz的毫米波连续波信号，阵列天线接收，天线远场条件为R≥L2/λ≈467 m.以直线阵所在直线为x轴，中心为原点，四个点目标极坐标分别为(49.5 m，0°)、(50 m，5°)、(51 m，-5°)、(50.5 m，0°)，运动速度(vx，vy)分别为(100，1000)、(500，600)、(600，-500)、(-500，-700)，其对应于原点的多普勒频率分别为-233.5 kHz、-149.74 kHz、128.51 kHz、163.44 kHz.信号采样频率为2.5 MHz，中频频率为500 kHz，各目标回波信号幅度相等，信噪比(SNR)为20 dB，快拍数为500，归一化频率搜索间隔取0.0001，距离与方位搜索间隔分别取0.05 m和0.001°，得信号的归一化频率估计及目标的距离、方位估计分别如图2、图3所示。计算的多普勒频率估计值为-233.5 kHz、-150.25 kHz、127.5 kHz、163.75 kHz，目标的距离与方位估计值为(49.6 m，0.012°)、(50.1 m，5.05°)、(50.85 m，-4.937°)、(50.45 m，-0.057°)。

图 2 频率谱估计

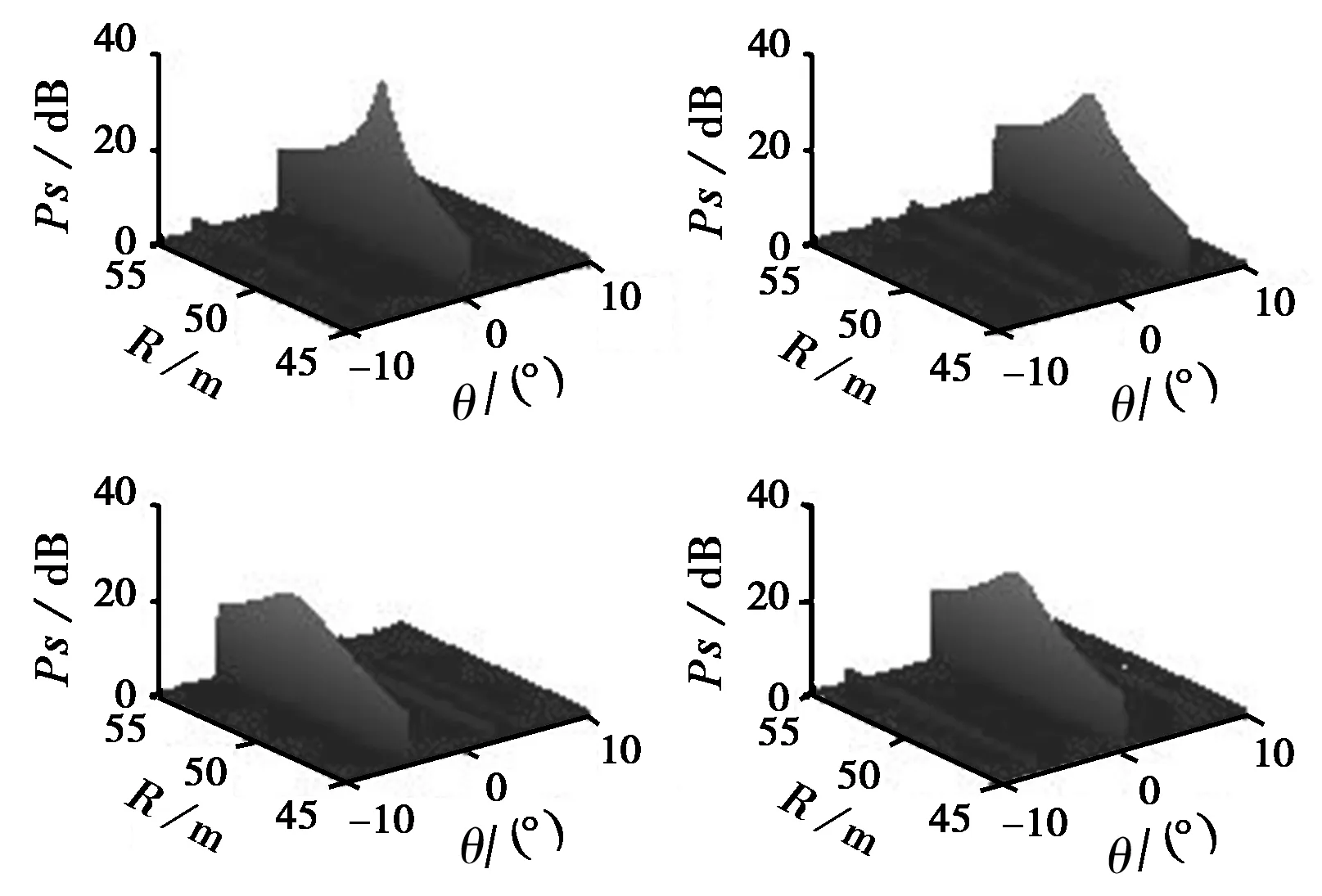
图 3 距离与方位估计

均方根误差(RMSE)如图 4所示。由图中估计结果可以看出，采用上节所述算法能有效估计近场中具有不同多普勒频率目标的多普勒频率、距离与方位，且具有很高的估计精度。从0 dB到30 dB改变SNR，每SNR作100次独立实验，得四个目标多普勒频率、距离与方位估计的RMSE。可以看出，在信噪比较低时，该算法能比较精确的估计目标的多普勒频率、距离和方位参数。

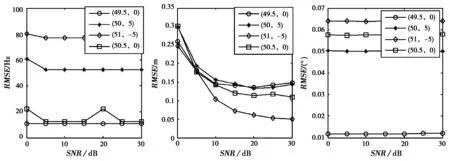
图 4 SNR变化时目标各个参数的RMSE

5. 结 论

针对近场动目标的定位问题，提出了一种主动式近场动目标的定位算法。首先采用MUSIC方法估计信号频率，根据动目标多普勒频率不同的特点对目标回波信号通过时域滤波加以分离，最后使用2D MUSIC算法估计目标的距离及方位参数。该算法可用于任意阵列，同时其可分辨目标数由频率可分辨数决定，可远大于阵元数。计算机仿真结果证明了算法的有效性。

[1] KRIM H, VIBERG M. Two decades of array signal processing research:the parametric approach[J]. IEEE Signal Processing Mag., 1996, 13(7): 67-94.

[2]HUANG Y D, BARKAT M. Near-field multiple source localization by passive sensor array[J]. IEEE Trans. Antennas and Propagation, 1991, 39(7): 968-975.

[3] YUEN N, FRIEDLANDER B. Higher-order ESPRIT for localization of near-field sources an asymptotic performance analysis[C]//8th IEEE Signal Processing Proceedings. Workshop on Statistical Signal and Array Processing, 1996: 538-541.

[4] HUANG Z, WANG S, WANG B. A Method for 4-D parameter estimation of near-field sources[C]//ICNSC '06. Proceedings of the 2006 IEEE International Conference on Networking, Sensing and Control, 2006: 997-1000.

[5] 陈建峰, 张贤达, 吴云韬. 近场源距离、频率及到达角联合估计算法[J]. 电子学报, 2004, 35(5): 803-806.

CHEN Jianfeng, ZHANG Xianda, WU Yuntao. An algorithm for jointly estimating range DOA and frequency of near field source[J]. Acta Electronica Sinica, 2004, 35(5): 803-806. (in Chinese)

[6] 梁军利, 王诗俊, 高 丽, 等. 一种无须参数配对的近场源定位新算法[J]. 电子学报, 2007, 35(6): 1122-1127.

LIANG Junli, WANG Shijun, GAO Li, et al. A new near-field source localization algorithm without pairing parameters[J]. Acta Electronica Sinica, 2007, 35(6): 1122-1127. (in Chinese)

[7] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans. Antennas and Propagation, 1986, 34(3): 276-280.

[8] 杨 鹏, 杨 峰, 聂在平, 等. MUSIC 算法在柱面共形天线阵DOA估计中的应用研究[J]. 电波科学学报, 2008, 23(2): 288-291.

YANG Peng, YANG Feng, NIE Zaiping, et al. DOA estimation of cylindrical conformal array by MUSIC algorithm[J]. Chinese Journal of Radio Science, 2008, 23(2): 288-291. (in Chinese)

[9] 王玲玲, 方大纲. 运用遗传算法综合稀疏阵列[J]. 电子学报, 2003, 31(12A): 2135-2138.

WANG Lingling, FANG Dagang. Genetic algorithm for the synthesis of thinned array[J]. ACTA Electronica Sinica, 2003, 31(12A): 2135-2138. (in Chinese)

[10] 尚 飞, 蔡亚星, 张 颖, 等. 阵列天线的双种群遗传算法综合[J]. 电波科学学报, 2007, 22(2): 224-228.

SHANG Fei, CAI Yaxing, ZHANG Ying, et al. Synthesis of array antenna using double population genetic algorithm[J]. Chinese Journal of Radio Science, 2007, 22(2): 224-228. (in Chinese)

[11] 欧阳骏, 杨 峰, 聂在平. 基于遗传算法的载体上共形天线阵列优化[J]. 电波科学学报, 2008, 23(2): 356-359.

OU Yangjun, YANG Feng, NIE Zaiping, et al. Optimizing Design of Conformal Antennas Array on Platform with GA Method[J]. Chinese Journal of Radio Science, 2008, 23(2): 356-359. (in Chinese)

[12] GODARA L C. Application of antenna arrays to mobile communications, part ii: beam-forming and direction-of-arrival considerations[J]. Proceedings of the IEEE, 1997, 85(8): 1195-1245.

[13] LIN J D, FANG W H, WANG Y Y, et al. FSF MUSIC for joint DOA and frequency estimation and its performance analysis[J]. IEEE Trans. Signal Processing, 2006, 54(12): 4529-4542.

[14] HORN A, JOHNSON C R. Matrixs Analysis[M]. U.K.: Cambridge Univ. Press, 1985.